题目内容
计算:(1)lg22+lg5•lg20-1;
(2)
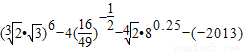 .
.
【答案】分析:(1)把lg5化为1-lg2,lg20化为1+lg2,展开平方差公式后整理即可;
(2)化根式为分数指数幂,化小数指数为分数指数,化负指数为正指数,然后进行有理指数幂的化简求值.
解答:解:(1)lg22+lg5•lg20-1
=lg22+(1-lg2)(1+lg2)-1
=lg22+1-lg22-1=0;
(2)
=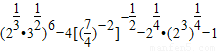
=
=22•33-7-2-1=98.
点评:本题考查了有理指数幂的化简与求值,考查了对数的运算性质,解答的关键是熟记有关性质,是基础题.
(2)化根式为分数指数幂,化小数指数为分数指数,化负指数为正指数,然后进行有理指数幂的化简求值.
解答:解:(1)lg22+lg5•lg20-1
=lg22+(1-lg2)(1+lg2)-1
=lg22+1-lg22-1=0;
(2)

=
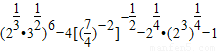
=

=22•33-7-2-1=98.
点评:本题考查了有理指数幂的化简与求值,考查了对数的运算性质,解答的关键是熟记有关性质,是基础题.

练习册系列答案
相关题目
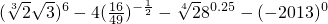 .
.