题目内容
（Ⅰ）用秦九韶算法求多项式f（x）=2x4+3x3+x2+5x-4，当x=2时的函数值．（Ⅱ）根据以下算法的程序，画出其相应的流程图
S=1
i=1
WHILE S＜=10000
i=i+2
S=S﹡i
WEND
PRINT i
END．
【答案】分析：（1）利用秦九韶算法计算多项式的值，先将多项式转化为f（x）=（（（2x+3）x+1）x+5）x-4的形式，然后逐步计算v至v4的值，即可得到答案．
（2）由于本题要根据计算算法的程序，故要采用选择结构来解决此问题，由于要讨论S与1000的大小关系，本题选择框中条件为：“S≤10000”即可．
解答：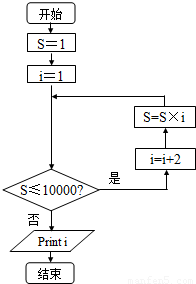
解：（1）f（x）=（（（2x+3）x+1）x+5）x-4
当x=2时，V1=2×2+3=7，V2=）=（2×2+3）×2+1=15，
同样V3=35，V4=66，
∴f（2）=66．
（2）相应的流程图为：如图所示．
点评：本题考查的知识点是秦九韶算法，流程图的概念，解答本题关键是掌握住本问题的解决方法，根据问题的解决方案制订出符合要求的框图，熟练掌握框图语言，能正确用框图把算法表示出来，这是设计流程图的基础．
（2）由于本题要根据计算算法的程序，故要采用选择结构来解决此问题，由于要讨论S与1000的大小关系，本题选择框中条件为：“S≤10000”即可．
解答：
解：（1）f（x）=（（（2x+3）x+1）x+5）x-4当x=2时，V1=2×2+3=7，V2=）=（2×2+3）×2+1=15，
同样V3=35，V4=66，
∴f（2）=66．
（2）相应的流程图为：如图所示．
点评：本题考查的知识点是秦九韶算法，流程图的概念，解答本题关键是掌握住本问题的解决方法，根据问题的解决方案制订出符合要求的框图，熟练掌握框图语言，能正确用框图把算法表示出来，这是设计流程图的基础．
练习册系列答案
名校课堂系列答案
相关题目