题目内容
如图，直线y=1与曲线y=-x2+2所围图形的面积是
【答案】分析：先根据题意画出的区域，然后依据图形交点得到积分下限，积分上限，从而利用定积分表示出曲边梯形的面积，最后用定积分的定义求出所求即可．
解答：解：根据所给图形，先将y=1代入y=-x2+2得：
得到积分上限为1，积分下限为-1，
直线y=1与曲线y=-x2+2所围图形的面积S=∫-11（2-x2-1）dx
而∫-11（1-x2）dx=（x-
）|-11=
∴所围图形的面积是
故答案为：
．
点评：本题主要考查了学生会求出原函数的能力，以及考查了数形结合的思想，同时会利用定积分求图形面积的能力，属于基础题．
解答：解：根据所给图形，先将y=1代入y=-x2+2得：
得到积分上限为1，积分下限为-1，
直线y=1与曲线y=-x2+2所围图形的面积S=∫-11（2-x2-1）dx
而∫-11（1-x2）dx=（x-
）|-11=∴所围图形的面积是
故答案为：
．点评：本题主要考查了学生会求出原函数的能力，以及考查了数形结合的思想，同时会利用定积分求图形面积的能力，属于基础题．
练习册系列答案
相关题目
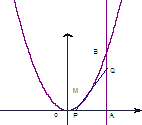
如图，由y=0，x=8，y=x2围成了曲边三角形OAB，M为曲线弧OB上一点，
（2007•广州一模）如图，已知曲线C1：y=x2与曲线C2：y=-x2+2ax（a＞1）交于点O，A，直线x=t（0＜t≤1）与曲线C1，C2分别相交于点D，B，连结OD，DA，AB，OB．
如图，由y=0，x=8，y=x2围成了曲边三角形OAB，M为曲线弧OB上一点，
