题目内容
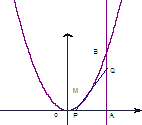 如图,由y=0,x=8,y=x2围成了曲边三角形OAB,M为曲线弧OB上一点,
如图,由y=0,x=8,y=x2围成了曲边三角形OAB,M为曲线弧OB上一点,设M点的横坐标为x0,过M作y=x2的切线PQ
(1)求PQ所在直线的方程(用x0表示);
(2)当PQ与OA,AB围成的三角形PQA面积最大时,求x0.
分析:(1)求出函数y=x2在M处的导数值,即切线PQ的斜率,利用点斜式写出直线PQ的方程.
(2)对于直线PQ的方程分别令y=0,x=8得到直线PQ与x轴的交点坐标及与直线x=8的交点坐标,利用两点距离公式求出三角形的两条直角边,利用三角形的面积表示出面积,对面积函数求导数,令导数等于0,判断出根左右两边的导函数符号,求出最大值.
(2)对于直线PQ的方程分别令y=0,x=8得到直线PQ与x轴的交点坐标及与直线x=8的交点坐标,利用两点距离公式求出三角形的两条直角边,利用三角形的面积表示出面积,对面积函数求导数,令导数等于0,判断出根左右两边的导函数符号,求出最大值.
解答:解:(1)f′(x0)=2x0 M(x0,x02)
∴PQ的方程2x0x-y-x02=0
(2)PQ的方程中,令y=0,x=
∴P(
,0)
∴|AP|=8-
PQ的方程中,令x=8,则y=16x0-x02
∴|AQ|=16x0-x02
.令S△PQA=u
∴u′=
x02-16x0+64
∴x0=
,x0=16(舍)
∵(0,
)是函数的增区(
,8)是函数的减区
∴x0=
时面积最大
∴PQ的方程2x0x-y-x02=0
(2)PQ的方程中,令y=0,x=
| x0 |
| 2 |
∴P(
| x0 |
| 2 |
∴|AP|=8-
| x0 |
| 2 |
PQ的方程中,令x=8,则y=16x0-x02
∴|AQ|=16x0-x02
.令S△PQA=u
∴u′=
| 3 |
| 4 |
∴x0=
| 16 |
| 3 |
∵(0,
| 16 |
| 3 |
| 16 |
| 3 |
∴x0=
| 16 |
| 3 |
点评:解决曲线的切线斜率问题,一般利用函数在切点处的导数值为切线的斜率;解决实际问题中的函数的最值问题,一般利用导数求出函数的极值即函数的最值.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案
相关题目
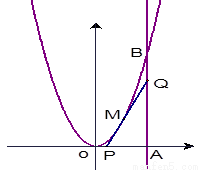
 如图,由y=0,x=8,y=x2围成了曲边三角形OAB,M为曲线弧OB上一点,
如图,由y=0,x=8,y=x2围成了曲边三角形OAB,M为曲线弧OB上一点,
