题目内容
设集合A为函数f(x)=ln(-x2-2x+8)的定义域,集合B为不等式(ax- )(x+4)≤0的解集.
)(x+4)≤0的解集.
(1) 写出f(x)的单调区间;
(2) 若B⊆∁R A,求a的取值范围.
 )(x+4)≤0的解集.
)(x+4)≤0的解集.(1) 写出f(x)的单调区间;
(2) 若B⊆∁R A,求a的取值范围.
(1)由-x2-2x+8>0,解得A=(-4,2),
单调递增区间为(-4,-1),单调递减区间(-1,2), ………………4分
(2)因为∁RA=(-∞,-4]∪[2,+∞). …………5分
由 (x+4)≤0,知a≠0. ………6分
(x+4)≤0,知a≠0. ………6分
①当a>0时,由 (x+4)≤0,得B=
(x+4)≤0,得B= ,不满足B⊆∁RA;……7分
,不满足B⊆∁RA;……7分
②当a<0时,由 (x+4)≥0,得B=(-∞,-4)∪
(x+4)≥0,得B=(-∞,-4)∪ ,
,
欲使B⊆∁RA,则 ≥2,解得-
≥2,解得- ≤a<0或0<a≤
≤a<0或0<a≤ ,
,
又a<0,所以- ≤a<0; …………9分
≤a<0; …………9分
综上所述,所求a的取值范围是 .
.
单调递增区间为(-4,-1),单调递减区间(-1,2), ………………4分
(2)因为∁RA=(-∞,-4]∪[2,+∞). …………5分
由
 (x+4)≤0,知a≠0. ………6分
(x+4)≤0,知a≠0. ………6分①当a>0时,由
 (x+4)≤0,得B=
(x+4)≤0,得B= ,不满足B⊆∁RA;……7分
,不满足B⊆∁RA;……7分②当a<0时,由
 (x+4)≥0,得B=(-∞,-4)∪
(x+4)≥0,得B=(-∞,-4)∪ ,
,欲使B⊆∁RA,则
 ≥2,解得-
≥2,解得- ≤a<0或0<a≤
≤a<0或0<a≤ ,
,又a<0,所以-
 ≤a<0; …………9分
≤a<0; …………9分综上所述,所求a的取值范围是
 .
.略

练习册系列答案
相关题目
 ,集合
,集合 ,
, ,那么集合
,那么集合 =___▲___.
=___▲___. 那么 ( )
那么 ( )



 的不等式:
的不等式: 解集为
解集为 ,若
,若 ,则实数
,则实数 的取值范围是( )
的取值范围是( )



 ,
, ,若
,若 ,则实数
,则实数 的取值范围是 。
的取值范围是 。
 集合
集合 则
则 等于
等于


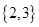
 ,若
,若 =R,则实数a的取值范围是( )
=R,则实数a的取值范围是( )