题目内容
下列说法:
①命题“存在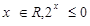 ” 的否定是“对任意的
” 的否定是“对任意的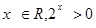 ”;
”;
②关于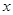 的不等式
的不等式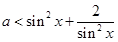 恒成立,则
恒成立,则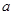 的取值范围是
的取值范围是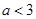 ;
;
③函数 为奇函数的充要条件是
为奇函数的充要条件是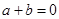 ;其中正确的个数是( )
;其中正确的个数是( )
| A.3 | B.2 | C.1 | D.0 |
B
解析试题分析:对于①,据含逻辑连接词的命题否定形式:“存在”变为“任意”,结论否定,故①对
对于②∵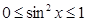 ,令
,令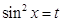 ,∴
,∴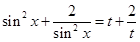 ,则令
,则令 ,
,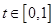 ,根据其图象可知,当
,根据其图象可知,当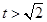 时,
时,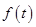 为递增的,当
为递增的,当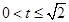 时,
时,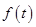 为递减的,∵
为递减的,∵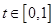 ,∴
,∴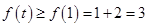 ,∴
,∴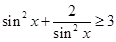 ∵
∵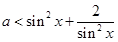 恒成立时,只要
恒成立时,只要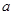 小于
小于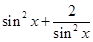 的最小值即可,
的最小值即可,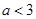 故②对;
故②对;
对于③当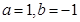 时,虽然有
时,虽然有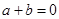 ,但
,但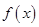 不是奇函数,故③错,故选B.
不是奇函数,故③错,故选B.
考点:命题的真假判断.

练习册系列答案
相关题目
“m=1”是“直线x-my=1和直线x+my=0互相垂直”的( )
| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
已知命题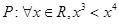 ,命题
,命题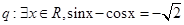 ,则下列命题中为真命题的是( )
,则下列命题中为真命题的是( )
A.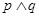 | B.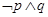 | C.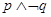 | D.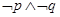 |
设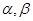 为两个不同平面,m、 n为两条不同的直线,且
为两个不同平面,m、 n为两条不同的直线,且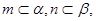 有两个命题:
有两个命题:
P:若m∥n,则 ∥β;q:若m⊥β, 则α⊥β. 那么( )
∥β;q:若m⊥β, 则α⊥β. 那么( )
| A.“p或q”是假命题 | B.“p且q”是真命题 |
| C.“非p或q”是假命题 | D.“非p且q”是真命题 |
命题
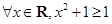 ,则
,则 是( )
是( )
A.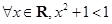 | B.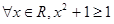 |
C.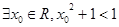 | D.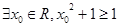 |
已知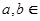 R,条件p:“
R,条件p:“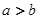 ”,条件q:“
”,条件q:“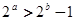 ”,则p是q的( )
”,则p是q的( )
| A.充分不必要条件 | B.必要不充分条件 |
| C.充分必要条件 | D.既不充分也不必要条件 |
下列说法中正确的是( )
A.“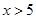 ”是“ ”是“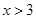 ”必要条件 ”必要条件 |
B.命题“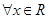 , ,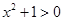 ”的否定是“ ”的否定是“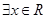 , ,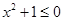 ” ” |
C.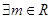 ,使函数 ,使函数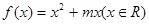 是奇函数 是奇函数 |
D.设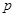 , ,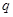 是简单命题,若 是简单命题,若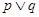 是真命题,则 是真命题,则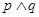 也是真命题 也是真命题 |
“ ”是“
”是“ ”的( )
”的( )
| A.充分不必要条件 | B.既不充分也不必要条件 |
| C.充要条件 | D.必要不充分条件 |
设x∈R,则“x>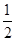 ”是“2x2+x-1>0”的( )
”是“2x2+x-1>0”的( )
| A.充分而不必要条件 | B.必要而不充分条件 |
| C.充分必要条件 | D.既不充分也不必要条件 |