题目内容
已知A,B是△ABC的两个内角,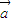 =
=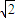 cos
cos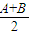
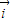 +sin
+sin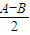
 (其中
(其中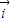 ,
,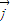 是互相垂直的单位向量),若|
是互相垂直的单位向量),若| |=
|=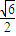 .
.(1)试问tanA•tanB是否为定值,若是定值,请求出,否则说明理由;
(2)求tanC的最大值,并判断此时三角形的形状.
【答案】分析:(1)利用向量模的公式得出关于角A,B的三角方程,利用二倍角公式、和差角公式化简三角方程,两边同除以cosAcosB得结论.
(2)据三角形的内角和为π,利用诱导公式求出tanC与tanA、tanB的关系,再利用基本不等式求出最大值.据三角形中,正切为负角为钝角,判断出三角形的形状.
解答:解:(1):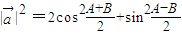 =
= ,
,
1+cos(A+B)+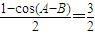
cosAcosB-sinAsinB-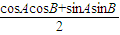 =0
=0
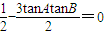 则tanAtanB=
则tanAtanB=
(2)由(1)可知A、B为锐角
tanC=-tan(B+A)=-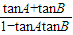 =
=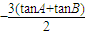
 =
=
所以tanC的最大值为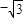
此时三角形ABC为钝角三角形.
点评:本题考查求 向量的模的坐标公式;三角函数的二倍角公式;三角函数的和差角公式;三角函数的同角公式;利用基本不等式求函数的最值.
(2)据三角形的内角和为π,利用诱导公式求出tanC与tanA、tanB的关系,再利用基本不等式求出最大值.据三角形中,正切为负角为钝角,判断出三角形的形状.
解答:解:(1):
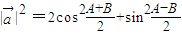 =
= ,
,1+cos(A+B)+
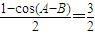
cosAcosB-sinAsinB-
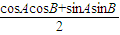 =0
=0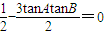 则tanAtanB=
则tanAtanB=
(2)由(1)可知A、B为锐角
tanC=-tan(B+A)=-
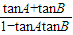 =
=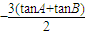
 =
=
所以tanC的最大值为
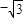
此时三角形ABC为钝角三角形.
点评:本题考查求 向量的模的坐标公式;三角函数的二倍角公式;三角函数的和差角公式;三角函数的同角公式;利用基本不等式求函数的最值.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目