题目内容
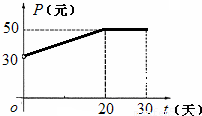
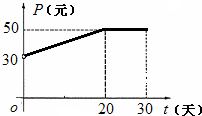 根据市场调查,某种新产品投放市场的30天内,每件销售价格P(元)与时间t(天 t∈N+)的关系满足如图,日销量Q(件)与时间t(天)之间的关系是Q=-t+40(t∈N+).
根据市场调查,某种新产品投放市场的30天内,每件销售价格P(元)与时间t(天 t∈N+)的关系满足如图,日销量Q(件)与时间t(天)之间的关系是Q=-t+40(t∈N+).(Ⅰ)写出该产品每件销售价格P与时间t的函数关系式;
(Ⅱ)在这30天内,哪一天的日销售金额最大?(日销量金额=每件产品销售价格×日销量)
分析:(I)根据图象,可得每件销售价格P与时间t的函数关系;
(II)结合日销量Q(件)与时间t(天)之间的关系,可得日销售金额函数,分段求最值,即可得到结论.
(II)结合日销量Q(件)与时间t(天)之间的关系,可得日销售金额函数,分段求最值,即可得到结论.
解答:解:(Ⅰ)根据图象,每件销售价格P与时间t的函数关系为:P=
.…(4分)
(Ⅱ)设日销售金额y(元),则y=
=
…(8分)
若0<t≤20,t∈N+时,y=-t2+10t+1200=-(t-5)2+1225,…(10分)
∴当t=5时,ymax=1225;
若20<t≤30,t∈N+时,y=-50t+2000是减函数,
∴y<-50×20+2000=1000,
因此,这种产品在第5天的日销售金额最大,最大日销售金额是1225元.…(12分)
|
(Ⅱ)设日销售金额y(元),则y=
|
=
|
若0<t≤20,t∈N+时,y=-t2+10t+1200=-(t-5)2+1225,…(10分)
∴当t=5时,ymax=1225;
若20<t≤30,t∈N+时,y=-50t+2000是减函数,
∴y<-50×20+2000=1000,
因此,这种产品在第5天的日销售金额最大,最大日销售金额是1225元.…(12分)
点评:本题考查函数模型的建立,考查函数的最值,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目
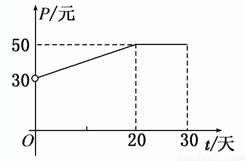
根据市场调查,某种新产品投放市场的30天内,每件销售价格P(元)与时间t(天)的关系如图所示,日销售量Q(件)与时间t(天)之间的关系如表所示.
(1)根据图象,写出该产品每件销售价格P与时间t的函数解析式;
(2)在所给的直角坐标系中,根据表中提供的数据描出实数对(t,Q)的对应点,并确定日销售量Q与时间t的一个函数解析式;
(3)在这30天内,哪一天的日销售金额最大?(日销售金额=每件产品销售价格×日销售量)

| t/天 | 5 | 15 | 20 | 30 |
| Q/件 | 35 | 25 | 20 | 10 |
(2)在所给的直角坐标系中,根据表中提供的数据描出实数对(t,Q)的对应点,并确定日销售量Q与时间t的一个函数解析式;
(3)在这30天内,哪一天的日销售金额最大?(日销售金额=每件产品销售价格×日销售量)

根据市场调查,某种新产品投放市场的30天内,每件销售价格P(元)与时间t(天)的关系如图所示,日销售量Q(件)与时间t(天)之间的关系如表所示.
(1)根据图象,写出该产品每件销售价格P与时间t的函数解析式;
(2)在所给的直角坐标系中,根据表中提供的数据描出实数对(t,Q)的对应点,并确定日销售量Q与时间t的一个函数解析式;
(3)在这30天内,哪一天的日销售金额最大?(日销售金额=每件产品销售价格×日销售量)
| t/天 | 5 | 15 | 20 | 30 |
| Q/件 | 35 | 25 | 20 | 10 |
(2)在所给的直角坐标系中,根据表中提供的数据描出实数对(t,Q)的对应点,并确定日销售量Q与时间t的一个函数解析式;
(3)在这30天内,哪一天的日销售金额最大?(日销售金额=每件产品销售价格×日销售量)

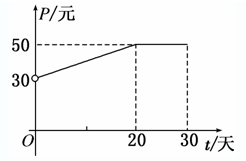 根据市场调查,某种新产品投放市场的30天内,每件销售价格P(元)与时间t(天)的关系如图所示,日销售量Q(件)与时间t(天)之间的关系如表所示.
根据市场调查,某种新产品投放市场的30天内,每件销售价格P(元)与时间t(天)的关系如图所示,日销售量Q(件)与时间t(天)之间的关系如表所示.