题目内容
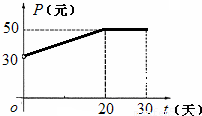
 根据市场调查,某种新产品投放市场的30天内,每件销售价格P(元)与时间t(天)的关系如图所示,日销售量Q(件)与时间t(天)之间的关系如表所示.
根据市场调查,某种新产品投放市场的30天内,每件销售价格P(元)与时间t(天)的关系如图所示,日销售量Q(件)与时间t(天)之间的关系如表所示.| t/天 | 5 | 15 | 20 | 30 |
| Q/件 | 35 | 25 | 20 | 10 |
(2)在所给的直角坐标系中,根据表中提供的数据描出实数对(t,Q)的对应点,并确定日销售量Q与时间t的一个函数解析式;
(3)在这30天内,哪一天的日销售金额最大?(日销售金额=每件产品销售价格×日销售量)
分析:(1)根据图象,每件销售价格P与时间t的函数关系为分段函数;
(2)设它们所在直线l的解析式,代入计算,可得结论;
(3)利用日销售金额=每件产品销售价格×日销售量,确定分段函数,分段求出函数的最值,即可求得结论.
(2)设它们所在直线l的解析式,代入计算,可得结论;
(3)利用日销售金额=每件产品销售价格×日销售量,确定分段函数,分段求出函数的最值,即可求得结论.
解答: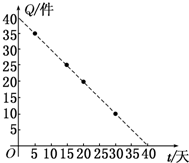 解:(1)根据图象,每件销售价格P与时间t的函数关系为:
解:(1)根据图象,每件销售价格P与时间t的函数关系为:
P=
;┅┅┅(2分)
(2)描出实数对(t,Q)对应点,如图所示.
从图象发现:点(5,35),(15,25),(20,20),(30,10)
可能在同一直线上.设它们所在直线l的解析式为Q=kt+b(k、b为常数),
将点(5,35),(30,10)代入方程得
解得k=-1,b=40,所以Q=-t+40,
检验点(15,25),(20,20)也适合该式,因此日销售量Q与时间t的一个解析式为
Q=-t+40(0<t≤30,t∈N+);┅┅┅┅┅┅┅┅┅┅┅┅┅┅(7分)
(3)设日销售金额为y(元),则y=
=
┅┅┅┅┅┅┅┅┅┅┅(9分)
若0<t≤20,t∈N+,y=-t2+10t+1200=-(t-5)2+1225,
所以当t=5时,ymax=1225;┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅(11分)
若20<t≤30,t∈N+,y=-50t+2000是减函数,所以y<-50×20+2000=1000.┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅(13分)
因此,这种产品在第5天的日销售金额最大,最大日销售金额是1225元.┅(14分)
 解:(1)根据图象,每件销售价格P与时间t的函数关系为:
解:(1)根据图象,每件销售价格P与时间t的函数关系为:P=
|
(2)描出实数对(t,Q)对应点,如图所示.
从图象发现:点(5,35),(15,25),(20,20),(30,10)
可能在同一直线上.设它们所在直线l的解析式为Q=kt+b(k、b为常数),
将点(5,35),(30,10)代入方程得
|
解得k=-1,b=40,所以Q=-t+40,
检验点(15,25),(20,20)也适合该式,因此日销售量Q与时间t的一个解析式为
Q=-t+40(0<t≤30,t∈N+);┅┅┅┅┅┅┅┅┅┅┅┅┅┅(7分)
(3)设日销售金额为y(元),则y=
|
=
|
若0<t≤20,t∈N+,y=-t2+10t+1200=-(t-5)2+1225,
所以当t=5时,ymax=1225;┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅(11分)
若20<t≤30,t∈N+,y=-50t+2000是减函数,所以y<-50×20+2000=1000.┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅(13分)
因此,这种产品在第5天的日销售金额最大,最大日销售金额是1225元.┅(14分)
点评:本题考查函数解析式的确定,考查函数的最值,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目
根据市场调查,某种新产品投放市场的30天内,每件销售价格P(元)与时间t(天)的关系如图所示,日销售量Q(件)与时间t(天)之间的关系如表所示.
(1)根据图象,写出该产品每件销售价格P与时间t的函数解析式;
(2)在所给的直角坐标系中,根据表中提供的数据描出实数对(t,Q)的对应点,并确定日销售量Q与时间t的一个函数解析式;
(3)在这30天内,哪一天的日销售金额最大?(日销售金额=每件产品销售价格×日销售量)

| t/天 | 5 | 15 | 20 | 30 |
| Q/件 | 35 | 25 | 20 | 10 |
(2)在所给的直角坐标系中,根据表中提供的数据描出实数对(t,Q)的对应点,并确定日销售量Q与时间t的一个函数解析式;
(3)在这30天内,哪一天的日销售金额最大?(日销售金额=每件产品销售价格×日销售量)

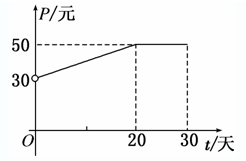
根据市场调查,某种新产品投放市场的30天内,每件销售价格P(元)与时间t(天)的关系如图所示,日销售量Q(件)与时间t(天)之间的关系如表所示.
(1)根据图象,写出该产品每件销售价格P与时间t的函数解析式;
(2)在所给的直角坐标系中,根据表中提供的数据描出实数对(t,Q)的对应点,并确定日销售量Q与时间t的一个函数解析式;
(3)在这30天内,哪一天的日销售金额最大?(日销售金额=每件产品销售价格×日销售量)
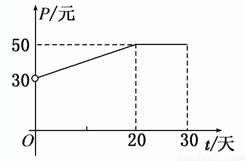
| t/天 | 5 | 15 | 20 | 30 |
| Q/件 | 35 | 25 | 20 | 10 |
(2)在所给的直角坐标系中,根据表中提供的数据描出实数对(t,Q)的对应点,并确定日销售量Q与时间t的一个函数解析式;
(3)在这30天内,哪一天的日销售金额最大?(日销售金额=每件产品销售价格×日销售量)

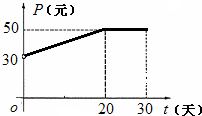 根据市场调查,某种新产品投放市场的30天内,每件销售价格P(元)与时间t(天 t∈N+)的关系满足如图,日销量Q(件)与时间t(天)之间的关系是Q=-t+40(t∈N+).
根据市场调查,某种新产品投放市场的30天内,每件销售价格P(元)与时间t(天 t∈N+)的关系满足如图,日销量Q(件)与时间t(天)之间的关系是Q=-t+40(t∈N+).