题目内容
A组:已知双曲线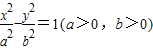 的离心率
的离心率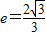 ,一条渐近线方程为
,一条渐近线方程为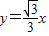 .
.(1)求双曲线C的方程
(2)过点(0,
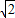 )倾斜角为45°的直线l与双曲线c恒有两个不同的交点A和B,求|AB|.
)倾斜角为45°的直线l与双曲线c恒有两个不同的交点A和B,求|AB|.B组:已知双曲线
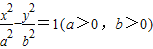 的离心率
的离心率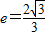 ,一条渐近线方程为
,一条渐近线方程为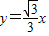 .
.(1)求双曲线C的方程
(2)过点(0,
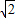 )是否存在一条直线l与双曲线c有两个不同交点A和B且
)是否存在一条直线l与双曲线c有两个不同交点A和B且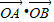 =2,若存在求出直线方程,若不存在请说明理由.
=2,若存在求出直线方程,若不存在请说明理由.
【答案】分析:A(1)由题设知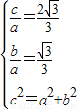 ,由此能求出双曲线C的方程.
,由此能求出双曲线C的方程.
(2)设直线l的方程为y=x+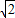 ,联立
,联立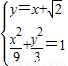 ,得4x2+6
,得4x2+6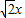 -3=0,再由弦长公式能求出|AB|.
-3=0,再由弦长公式能求出|AB|.
B(1)由题设知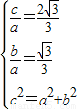 ,由此能求出双曲线C的方程.
,由此能求出双曲线C的方程.
(2)假设直线l存在.设直线l的方程为y=kx+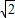 ,联立
,联立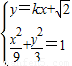 ,得(3k2+1)x2+6
,得(3k2+1)x2+6 -3=0,由
-3=0,由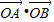 =2,得k2=-
=2,得k2=- .不成立.故不存在一条直线l与双曲线c有两个不同交点A和B且
.不成立.故不存在一条直线l与双曲线c有两个不同交点A和B且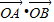 =2.
=2.
解答:解:A(1)∵双曲线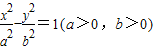 的离心率
的离心率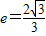 ,
,
一条渐近线方程为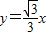 ,
,
∴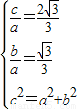 ,解得a2=9,b2=3,
,解得a2=9,b2=3,
∴双曲线C的方程为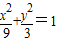 .
.
(2)过点(0,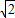 )倾斜角为45°的直线l的方程为y=x+
)倾斜角为45°的直线l的方程为y=x+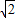 ,
,
联立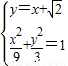 ,得4x2+6
,得4x2+6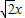 -3=0,
-3=0,
△=(6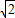 )2+4×4×3=120,
)2+4×4×3=120,
设A(x1,y1),B(x2,y2),则x1+x2=-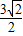 ,x1x2=-
,x1x2=- ,k=tan45°=1,
,k=tan45°=1,
∴|AB|=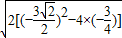 =
= .
.
BA(1)∵双曲线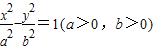 的离心率
的离心率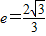 ,
,
一条渐近线方程为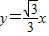 ,
,
∴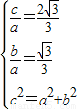 ,解得a2=9,b2=3,
,解得a2=9,b2=3,
∴双曲线C的方程为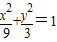 .
.
(2)假设直线l存在.设直线l的方程为y=kx+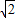 ,
,
联立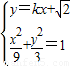 ,得(3k2+1)x2+6
,得(3k2+1)x2+6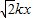 -3=0,
-3=0,
∵直线l与双曲线c有两个不同交点A和B,
∴△=(6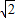 k)2+4×(3k2+1)×3>0,k∈R.
k)2+4×(3k2+1)×3>0,k∈R.
设A(x1,y1),B(x2,y2),则x1+x2=-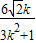 ,x1x2=-
,x1x2=-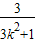 ,
,
y1y2=(kx1+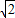 )(kx2+
)(kx2+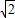 )=k2x1x2+
)=k2x1x2+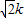 (x1+x2)+2
(x1+x2)+2
=-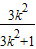 -
- +2
+2
=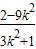 .
.
∵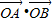 =2,
=2,
∴x1x2+y1y2=-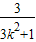 +
+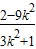 =
=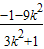 =2,
=2,
整理,得k2=- .不成立.
.不成立.
故不存在一条直线l与双曲线c有两个不同交点A和B且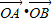 =2.
=2.
点评:本题考查椭圆方程的求法,考查弦长的求法,考查直线是否存在的判断.综合性强,难度大,在一定的探索性,解题时要认真审题,仔细解答,注意等价转化思想的合理运用.
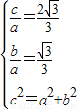 ,由此能求出双曲线C的方程.
,由此能求出双曲线C的方程.(2)设直线l的方程为y=x+
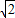 ,联立
,联立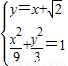 ,得4x2+6
,得4x2+6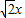 -3=0,再由弦长公式能求出|AB|.
-3=0,再由弦长公式能求出|AB|.B(1)由题设知
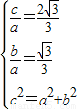 ,由此能求出双曲线C的方程.
,由此能求出双曲线C的方程.(2)假设直线l存在.设直线l的方程为y=kx+
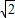 ,联立
,联立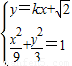 ,得(3k2+1)x2+6
,得(3k2+1)x2+6 -3=0,由
-3=0,由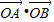 =2,得k2=-
=2,得k2=- .不成立.故不存在一条直线l与双曲线c有两个不同交点A和B且
.不成立.故不存在一条直线l与双曲线c有两个不同交点A和B且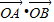 =2.
=2.解答:解:A(1)∵双曲线
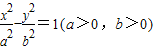 的离心率
的离心率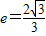 ,
,一条渐近线方程为
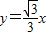 ,
,∴
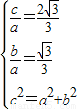 ,解得a2=9,b2=3,
,解得a2=9,b2=3,∴双曲线C的方程为
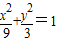 .
.(2)过点(0,
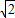 )倾斜角为45°的直线l的方程为y=x+
)倾斜角为45°的直线l的方程为y=x+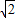 ,
,联立
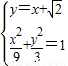 ,得4x2+6
,得4x2+6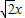 -3=0,
-3=0,△=(6
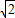 )2+4×4×3=120,
)2+4×4×3=120,设A(x1,y1),B(x2,y2),则x1+x2=-
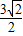 ,x1x2=-
,x1x2=- ,k=tan45°=1,
,k=tan45°=1,∴|AB|=
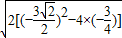 =
= .
.BA(1)∵双曲线
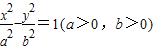 的离心率
的离心率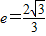 ,
,一条渐近线方程为
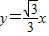 ,
,∴
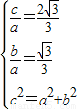 ,解得a2=9,b2=3,
,解得a2=9,b2=3,∴双曲线C的方程为
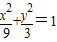 .
.(2)假设直线l存在.设直线l的方程为y=kx+
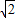 ,
,联立
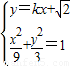 ,得(3k2+1)x2+6
,得(3k2+1)x2+6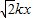 -3=0,
-3=0,∵直线l与双曲线c有两个不同交点A和B,
∴△=(6
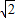 k)2+4×(3k2+1)×3>0,k∈R.
k)2+4×(3k2+1)×3>0,k∈R.设A(x1,y1),B(x2,y2),则x1+x2=-
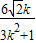 ,x1x2=-
,x1x2=-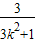 ,
,y1y2=(kx1+
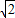 )(kx2+
)(kx2+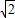 )=k2x1x2+
)=k2x1x2+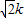 (x1+x2)+2
(x1+x2)+2=-
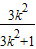 -
- +2
+2=
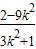 .
.∵
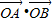 =2,
=2,∴x1x2+y1y2=-
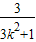 +
+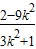 =
=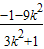 =2,
=2,整理,得k2=-
 .不成立.
.不成立.故不存在一条直线l与双曲线c有两个不同交点A和B且
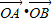 =2.
=2.点评:本题考查椭圆方程的求法,考查弦长的求法,考查直线是否存在的判断.综合性强,难度大,在一定的探索性,解题时要认真审题,仔细解答,注意等价转化思想的合理运用.

练习册系列答案
 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
相关题目
 如图,已知|AB|=10,图中的一系列圆是圆心分别为A、B的两组同心圆,每组同心圆的半径分别是1,2,3,…,n,….利用这两组同心圆可以画出以A、B为焦点的双曲线.若其中经过点M、N、P的双曲线的离心率分别是eM,eN,eP.则它们的大小关系是
如图,已知|AB|=10,图中的一系列圆是圆心分别为A、B的两组同心圆,每组同心圆的半径分别是1,2,3,…,n,….利用这两组同心圆可以画出以A、B为焦点的双曲线.若其中经过点M、N、P的双曲线的离心率分别是eM,eN,eP.则它们的大小关系是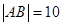 ,图中的一系列圆是圆心分别为A、B的两组同心圆,每组同心圆的半径分别是1,2,3,…,n,….利用这两组同心圆可以画出以A、B为焦点的双曲线. 若其中经过点M、N、P的双曲线的离心率分别是
,图中的一系列圆是圆心分别为A、B的两组同心圆,每组同心圆的半径分别是1,2,3,…,n,….利用这两组同心圆可以画出以A、B为焦点的双曲线. 若其中经过点M、N、P的双曲线的离心率分别是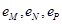 .则它们的大小关系是
(用“
.则它们的大小关系是
(用“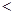 ”连接).
”连接).
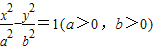 的离心率
的离心率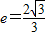 ,一条渐近线方程为
,一条渐近线方程为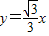 .
.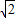 )倾斜角为45°的直线l与双曲线c恒有两个不同的交点A和B,求|AB|.
)倾斜角为45°的直线l与双曲线c恒有两个不同的交点A和B,求|AB|. 的离心率
的离心率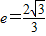 ,一条渐近线方程为
,一条渐近线方程为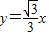 .
.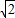 )是否存在一条直线l与双曲线c有两个不同交点A和B且
)是否存在一条直线l与双曲线c有两个不同交点A和B且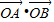 =2,若存在求出直线方程,若不存在请说明理由.
=2,若存在求出直线方程,若不存在请说明理由.