ĚâÄżÄÚČÝ
A×飺ŇŃÖŞË«ÇúĎß
-
=1(aŁľ0Ł¬bŁľ0)µÄŔëĐÄÂĘe=
Ł¬Ň»Ěő˝Ą˝üĎß·˝łĚÎŞy=
xŁ®
Ł¨1Ł©ÇóË«ÇúĎßCµÄ·˝łĚ
Ł¨2Ł©ąýµăŁ¨0Ł¬
Ł©Çăб˝ÇÎŞ45ˇăµÄÖ±ĎßlÓëË«ÇúĎßcşăÓĐÁ˝¸ö˛»Í¬µÄ˝»µăAşÍBŁ¬Çó|AB|Ł®
B×飺ŇŃÖŞË«ÇúĎß
-
=1(aŁľ0Ł¬bŁľ0)µÄŔëĐÄÂĘe=
Ł¬Ň»Ěő˝Ą˝üĎß·˝łĚÎŞy=
xŁ®
Ł¨1Ł©ÇóË«ÇúĎßCµÄ·˝łĚ
Ł¨2Ł©ąýµăŁ¨0Ł¬
Ł©ĘÇ·ń´ćÔÚŇ»ĚőÖ±ĎßlÓëË«ÇúĎßcÓĐÁ˝¸ö˛»Í¬˝»µăAşÍBÇŇ
•
=2Ł¬Čô´ćÔÚÇółöÖ±Ďß·˝łĚŁ¬Čô˛»´ćÔÚÇë˵Ă÷ŔíÓÉŁ®
| x2 |
| a2 |
| y2 |
| b2 |
2
| ||
| 3 |
| ||
| 3 |
Ł¨1Ł©ÇóË«ÇúĎßCµÄ·˝łĚ
Ł¨2Ł©ąýµăŁ¨0Ł¬
| 2 |
B×飺ŇŃÖŞË«ÇúĎß
| x2 |
| a2 |
| y2 |
| b2 |
2
| ||
| 3 |
| ||
| 3 |
Ł¨1Ł©ÇóË«ÇúĎßCµÄ·˝łĚ
Ł¨2Ł©ąýµăŁ¨0Ł¬
| 2 |
| OA |
| OB |
·ÖÎöŁşAŁ¨1Ł©ÓÉĚâÉčÖŞ
Ł¬ÓÉ´ËÄÜÇółöË«ÇúĎßCµÄ·˝łĚŁ®
Ł¨2Ł©ÉčÖ±ĎßlµÄ·˝łĚÎŞy=x+
Ł¬ÁŞÁ˘
Ł¬µĂ4x2+6
x-3=0Ł¬ÔŮÓÉĎŇł¤ą«Ę˝ÄÜÇółö|AB|Ł®
BŁ¨1Ł©ÓÉĚâÉčÖŞ
Ł¬ÓÉ´ËÄÜÇółöË«ÇúĎßCµÄ·˝łĚŁ®
Ł¨2Ł©ĽŮÉčÖ±Ďßl´ćÔÚŁ®ÉčÖ±ĎßlµÄ·˝łĚÎŞy=kx+
Ł¬ÁŞÁ˘
Ł¬µĂŁ¨3k2+1Ł©x2+6
kx-3=0Ł¬ÓÉ
•
=2Ł¬µĂk2=-
Ł®˛»łÉÁ˘Ł®ąĘ˛»´ćÔÚŇ»ĚőÖ±ĎßlÓëË«ÇúĎßcÓĐÁ˝¸ö˛»Í¬˝»µăAşÍBÇŇ
•
=2Ł®
|
Ł¨2Ł©ÉčÖ±ĎßlµÄ·˝łĚÎŞy=x+
| 2 |
|
| 2 |
BŁ¨1Ł©ÓÉĚâÉčÖŞ
|
Ł¨2Ł©ĽŮÉčÖ±Ďßl´ćÔÚŁ®ÉčÖ±ĎßlµÄ·˝łĚÎŞy=kx+
| 2 |
|
| 2 |
| OA |
| OB |
| 1 |
| 5 |
| OA |
| OB |
˝â´đŁş˝âŁşAŁ¨1Ł©ˇßË«ÇúĎß
-
=1(aŁľ0Ł¬bŁľ0)µÄŔëĐÄÂĘe=
Ł¬
Ň»Ěő˝Ą˝üĎß·˝łĚÎŞy=
xŁ¬
ˇŕ
Ł¬˝âµĂa2=9Ł¬b2=3Ł¬
ˇŕË«ÇúĎßCµÄ·˝łĚÎŞ
+
=1Ł®
Ł¨2Ł©ąýµăŁ¨0Ł¬
Ł©Çăб˝ÇÎŞ45ˇăµÄÖ±ĎßlµÄ·˝łĚÎŞy=x+
Ł¬
ÁŞÁ˘
Ł¬µĂ4x2+6
x-3=0Ł¬
ˇ÷=Ł¨6
Ł©2+4ˇÁ4ˇÁ3=120Ł¬
ÉčAŁ¨x1Ł¬y1Ł©Ł¬BŁ¨x2Ł¬y2Ł©Ł¬Ôňx1+x2=-
Ł¬x1x2=-
Ł¬k=tan45ˇă=1Ł¬
ˇŕ|AB|=
=
Ł®
BAŁ¨1Ł©ˇßË«ÇúĎß
-
=1(aŁľ0Ł¬bŁľ0)µÄŔëĐÄÂĘe=
Ł¬
Ň»Ěő˝Ą˝üĎß·˝łĚÎŞy=
xŁ¬
ˇŕ
Ł¬˝âµĂa2=9Ł¬b2=3Ł¬
ˇŕË«ÇúĎßCµÄ·˝łĚÎŞ
+
=1Ł®
Ł¨2Ł©ĽŮÉčÖ±Ďßl´ćÔÚŁ®ÉčÖ±ĎßlµÄ·˝łĚÎŞy=kx+
Ł¬
ÁŞÁ˘
Ł¬µĂŁ¨3k2+1Ł©x2+6
kx-3=0Ł¬
ˇßÖ±ĎßlÓëË«ÇúĎßcÓĐÁ˝¸ö˛»Í¬˝»µăAşÍBŁ¬
ˇŕˇ÷=Ł¨6
kŁ©2+4ˇÁŁ¨3k2+1Ł©ˇÁ3Łľ0Ł¬kˇĘRŁ®
ÉčAŁ¨x1Ł¬y1Ł©Ł¬BŁ¨x2Ł¬y2Ł©Ł¬Ôňx1+x2=-
Ł¬x1x2=-
Ł¬
y1y2=Ł¨kx1+
Ł©Ł¨kx2+
Ł©=k2x1x2+
kŁ¨x1+x2Ł©+2
=-
-
+2
=
Ł®
ˇß
•
=2Ł¬
ˇŕx1x2+y1y2=-
+
=
=2Ł¬
ŐűŔíŁ¬µĂk2=-
Ł®˛»łÉÁ˘Ł®
ąĘ˛»´ćÔÚŇ»ĚőÖ±ĎßlÓëË«ÇúĎßcÓĐÁ˝¸ö˛»Í¬˝»µăAşÍBÇŇ
•
=2Ł®
| x2 |
| a2 |
| y2 |
| b2 |
2
| ||
| 3 |
Ň»Ěő˝Ą˝üĎß·˝łĚÎŞy=
| ||
| 3 |
ˇŕ
|
ˇŕË«ÇúĎßCµÄ·˝łĚÎŞ
| x2 |
| 9 |
| y2 |
| 3 |
Ł¨2Ł©ąýµăŁ¨0Ł¬
| 2 |
| 2 |
ÁŞÁ˘
|
| 2 |
ˇ÷=Ł¨6
| 2 |
ÉčAŁ¨x1Ł¬y1Ł©Ł¬BŁ¨x2Ł¬y2Ł©Ł¬Ôňx1+x2=-
3
| ||
| 2 |
| 3 |
| 4 |
ˇŕ|AB|=
2[(-
|
| 15 |
BAŁ¨1Ł©ˇßË«ÇúĎß
| x2 |
| a2 |
| y2 |
| b2 |
2
| ||
| 3 |
Ň»Ěő˝Ą˝üĎß·˝łĚÎŞy=
| ||
| 3 |
ˇŕ
|
ˇŕË«ÇúĎßCµÄ·˝łĚÎŞ
| x2 |
| 9 |
| y2 |
| 3 |
Ł¨2Ł©ĽŮÉčÖ±Ďßl´ćÔÚŁ®ÉčÖ±ĎßlµÄ·˝łĚÎŞy=kx+
| 2 |
ÁŞÁ˘
|
| 2 |
ˇßÖ±ĎßlÓëË«ÇúĎßcÓĐÁ˝¸ö˛»Í¬˝»µăAşÍBŁ¬
ˇŕˇ÷=Ł¨6
| 2 |
ÉčAŁ¨x1Ł¬y1Ł©Ł¬BŁ¨x2Ł¬y2Ł©Ł¬Ôňx1+x2=-
6
| ||
| 3k2+1 |
| 3 |
| 3k2+1 |
y1y2=Ł¨kx1+
| 2 |
| 2 |
| 2 |
=-
| 3k2 |
| 3k2+1 |
| 12k2 |
| 3k2+1 |
=
| 2-9k2 |
| 3k2+1 |
ˇß
| OA |
| OB |
ˇŕx1x2+y1y2=-
| 3 |
| 3k2+1 |
| 2-9k2 |
| 3k2+1 |
| -1-9k2 |
| 3k2+1 |
ŐűŔíŁ¬µĂk2=-
| 1 |
| 5 |
ąĘ˛»´ćÔÚŇ»ĚőÖ±ĎßlÓëË«ÇúĎßcÓĐÁ˝¸ö˛»Í¬˝»µăAşÍBÇŇ
| OA |
| OB |
µăĆŔŁş±ľĚ⿼˛éÍÖÔ˛·˝łĚµÄÇ󷨣¬żĽ˛éĎŇł¤µÄÇ󷨣¬żĽ˛éÖ±ĎßĘÇ·ń´ćÔÚµÄĹжϣ®×ŰşĎĐÔÇżŁ¬ÄѶȴóŁ¬ÔÚŇ»¶¨µÄĚ˝Ë÷ĐÔŁ¬˝âĚâʱҪČĎŐćÉóĚ⣬×Đϸ˝â´đŁ¬×˘ŇâµČĽŰת»ŻËĽĎëµÄşĎŔíÔËÓĂŁ®

Á·Ď°˛áϵÁĐ´đ°¸
 ŃôąâżĽłˇµĄÔŞ˛âĘÔľíϵÁĐ´đ°¸
ŃôąâżĽłˇµĄÔŞ˛âĘÔľíϵÁĐ´đ°¸ ĂűĐŁÁŞĂËłĺ´ĚľíϵÁĐ´đ°¸
ĂűĐŁÁŞĂËłĺ´ĚľíϵÁĐ´đ°¸ ĂűĐŁĚá·ÖŇ»ľíͨϵÁĐ´đ°¸
ĂűĐŁĚá·ÖŇ»ľíͨϵÁĐ´đ°¸
ĎŕąŘĚâÄż
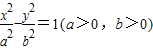 µÄŔëĐÄÂĘ
µÄŔëĐÄÂĘ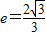 Ł¬Ň»Ěő˝Ą˝üĎß·˝łĚÎŞ
Ł¬Ň»Ěő˝Ą˝üĎß·˝łĚÎŞ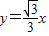 Ł®
Ł®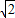 Ł©Çăб˝ÇÎŞ45°µÄÖ±ĎßlÓëË«ÇúĎßcşăÓĐÁ˝¸ö˛»Í¬µÄ˝»µăAşÍBŁ¬Çó|AB|Ł®
Ł©Çăб˝ÇÎŞ45°µÄÖ±ĎßlÓëË«ÇúĎßcşăÓĐÁ˝¸ö˛»Í¬µÄ˝»µăAşÍBŁ¬Çó|AB|Ł®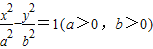 µÄŔëĐÄÂĘ
µÄŔëĐÄÂĘ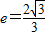 Ł¬Ň»Ěő˝Ą˝üĎß·˝łĚÎŞ
Ł¬Ň»Ěő˝Ą˝üĎß·˝łĚÎŞ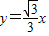 Ł®
Ł®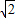 Ł©ĘÇ·ń´ćÔÚŇ»ĚőÖ±ĎßlÓëË«ÇúĎßcÓĐÁ˝¸ö˛»Í¬˝»µăAşÍBÇŇ
Ł©ĘÇ·ń´ćÔÚŇ»ĚőÖ±ĎßlÓëË«ÇúĎßcÓĐÁ˝¸ö˛»Í¬˝»µăAşÍBÇŇ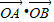 =2Ł¬Čô´ćÔÚÇółöÖ±Ďß·˝łĚŁ¬Čô˛»´ćÔÚÇë˵Ă÷ŔíÓÉŁ®
=2Ł¬Čô´ćÔÚÇółöÖ±Ďß·˝łĚŁ¬Čô˛»´ćÔÚÇë˵Ă÷ŔíÓÉŁ®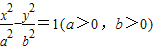 µÄŔëĐÄÂĘ
µÄŔëĐÄÂĘ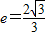 Ł¬Ň»Ěő˝Ą˝üĎß·˝łĚÎŞ
Ł¬Ň»Ěő˝Ą˝üĎß·˝łĚÎŞ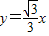 Ł®
Ł®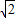 Ł©Çăб˝ÇÎŞ45°µÄÖ±ĎßlÓëË«ÇúĎßcşăÓĐÁ˝¸ö˛»Í¬µÄ˝»µăAşÍBŁ¬Çó|AB|Ł®
Ł©Çăб˝ÇÎŞ45°µÄÖ±ĎßlÓëË«ÇúĎßcşăÓĐÁ˝¸ö˛»Í¬µÄ˝»µăAşÍBŁ¬Çó|AB|Ł® µÄŔëĐÄÂĘ
µÄŔëĐÄÂĘ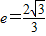 Ł¬Ň»Ěő˝Ą˝üĎß·˝łĚÎŞ
Ł¬Ň»Ěő˝Ą˝üĎß·˝łĚÎŞ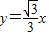 Ł®
Ł®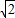 Ł©ĘÇ·ń´ćÔÚŇ»ĚőÖ±ĎßlÓëË«ÇúĎßcÓĐÁ˝¸ö˛»Í¬˝»µăAşÍBÇŇ
Ł©ĘÇ·ń´ćÔÚŇ»ĚőÖ±ĎßlÓëË«ÇúĎßcÓĐÁ˝¸ö˛»Í¬˝»µăAşÍBÇŇ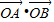 =2Ł¬Čô´ćÔÚÇółöÖ±Ďß·˝łĚŁ¬Čô˛»´ćÔÚÇë˵Ă÷ŔíÓÉŁ®
=2Ł¬Čô´ćÔÚÇółöÖ±Ďß·˝łĚŁ¬Čô˛»´ćÔÚÇë˵Ă÷ŔíÓÉŁ®