题目内容
下面四个图案,都是由小正三角形构成,设第n个图形中所有小正三角形边上黑点的总数为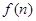 .
.
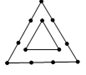
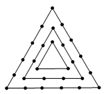
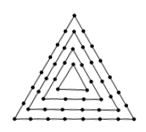
图1 图2 图3 图4
(1)求出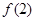 ,
,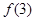 ,
,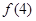 ,
,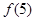 ;
;
(2)找出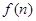 与
与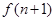 的关系,并求出
的关系,并求出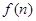 的表达式;
的表达式;
(3)求证: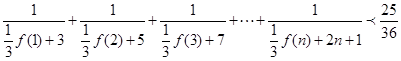 (
( ).
).
(1)12,27,48,75.
(2)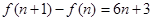 ,
, 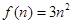 .
.
(3)利用“放缩法”。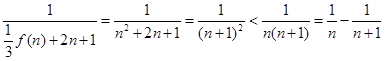 .
.
解析试题分析:(1)由题意有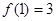 ,
,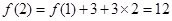 ,
,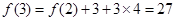 ,
,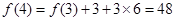 ,
,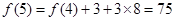 . 2分
. 2分
(2)由题意及(1)知,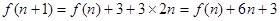 , 4分
, 4分
即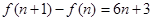 ,
,
所以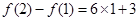 ,
,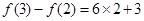 ,
,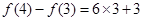 ,
,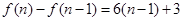 , 5分
, 5分
将上面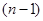 个式子相加,得:
个式子相加,得: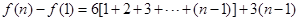
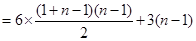
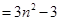 6分
6分
又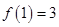 ,所以
,所以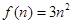 . 7分
. 7分
(3)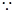
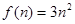
∴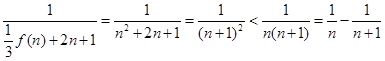 . 9分
. 9分
当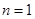 时,
时,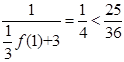 ,原不等式成立. 10分
,原不等式成立. 10分
当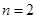 时,
时,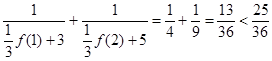 ,原不等式成立. 11分
,原不等式成立. 11分
当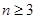 时,
时,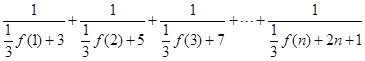
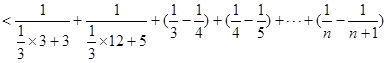
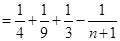
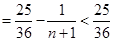 , 原不等式成立. 13分
, 原不等式成立. 13分
综上所述,对于任意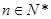 ,原不等式成立. 14分
,原不等式成立. 14分
考点:归纳推理,不等式的证明,“裂项相消法”。
点评:中档题,本题综合性较强,注意从图形出发,发现规律,确定“递推关系”。不等式的证明问题,往往需要先放缩,后求和,再证明。

练习册系列答案
 激活思维优加课堂系列答案
激活思维优加课堂系列答案 活力试卷系列答案
活力试卷系列答案
相关题目
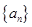 满足
满足 ,
, .
. 的前n项和.
的前n项和. +
+ +…+
+…+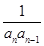 <
<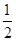 .
. 的首项
的首项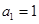 ,公差
,公差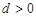 .且
.且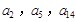 分别是等比数列
分别是等比数列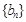 的
的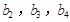 .
. 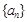 与
与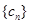 对任意自然数
对任意自然数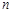 均有
均有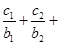
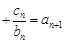 成立,求
成立,求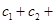
 的值.
的值.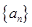 满足
满足 (
( 为常数),
为常数),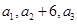 成等差数列.
成等差数列. 满足
满足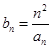 ,证明:
,证明: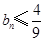 .
. 的前
的前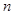 项和为
项和为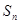 ,已知
,已知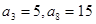 .
. ;
;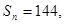 求
求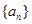 的前
的前 项和为
项和为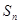 ,且
,且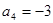 ,
,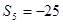
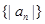 的前
的前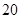 项和
项和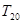 .
.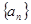 满足
满足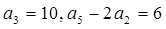 .
.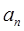 ;
; 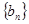 满足
满足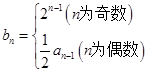 ,
, 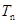 为数列
为数列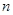 项和,求
项和,求 .
. 中,
中, ,前
,前 项的和为
项的和为 ,对任意的
,对任意的 ,
, ,
, ,
, 总成等差数列.
总成等差数列. 的值;
的值; .
.