题目内容
若x≠0，则x+
的取值范围为________．
（-∞，-2]∪[2，+∞）
分析：对x分x＞0与x＜0，利用基本不等式即可求得答案．
解答：∵x≠0，
∴当x＞0时，x+≥2
=2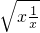（当且仅当x=1时取“=”）；
当x＜0时，-x＞0，
∴-x-≥2（当且仅当x=-1时取“=”）；
∴x+≤-2．
综上所述，x+的取值范围为（-∞，-2]∪[2，+∞）．
故答案为；（-∞，-2]∪[2，+∞）．
点评：本题考查基本不等式，考查分类讨论思想的运用，属于基础题．
分析：对x分x＞0与x＜0，利用基本不等式即可求得答案．
解答：∵x≠0，
∴当x＞0时，x+
≥2=2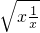（当且仅当x=1时取“=”）；当x＜0时，-x＞0，
∴-x-
≥2（当且仅当x=-1时取“=”）；∴x+
≤-2．综上所述，x+
的取值范围为（-∞，-2]∪[2，+∞）．故答案为；（-∞，-2]∪[2，+∞）．
点评：本题考查基本不等式，考查分类讨论思想的运用，属于基础题．
练习册系列答案
相关题目
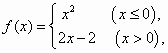若f(x)≥0，则x的取值范围是