题目内容
设e1,e2,e3,e4是某平面内的四个单位向量,其中e1⊥e2,e3与e4的夹角为45°,对这个平面内的任意一个向量a=xe1+ye2,规定经过一次“斜二测变换”得到向量a1=xe3+ e4.设向量t1=-3e3-2e4是经过一次“斜二测变换”得到的向量,则|t|是( )
e4.设向量t1=-3e3-2e4是经过一次“斜二测变换”得到的向量,则|t|是( )
| A.5 | B.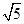 | C.73 | D. |
A
解析

练习册系列答案
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案
相关题目
若平面向量 与
与 ,
, ,
,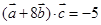 ,则
,则 与
与 的夹角为( )
的夹角为( )
A. | B. | C. | D.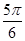 |
已知 、
、 是两个单位向量,下列四个命题中正确的是 ( )
是两个单位向量,下列四个命题中正确的是 ( )
A. 与 与 相等 相等 | B.如果 与 与 平行,那么 平行,那么 与 与 相等 相等 |
C. · · =1 =1 | D. = = |
若 (
( )是
)是 所在的平面内的点,且
所在的平面内的点,且 .
.
给出下列说法:①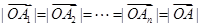 ;②
;② 的最小值一定是
的最小值一定是 ;
;
③点 、
、 在一条直线上.其中正确的个数是( )
在一条直线上.其中正确的个数是( )
A. 个. 个. | B. 个. 个. | C. 个. 个. | D. 个. 个. |
在 中,
中,  ,则下列等式成立的是( )
,则下列等式成立的是( )
A. | B. | C. | D. |
在直角梯形 中,
中, ,
, ,
, ,
, ,点
,点 在线段
在线段 上,若
上,若 ,则
,则 的取值范围是( )
的取值范围是( )
A. | B. | C. | D. |
设A,B,C,D是空间不共面的四个点,且满足 ·
· =0,
=0, ·
· =0,
=0, ·
· =0,则△BCD的形状是( )
=0,则△BCD的形状是( )
| A.钝角三角形 | B.直角三角形 |
| C.锐角三角形 | D.无法确定 |
 是两个非零向量,则下列命题为真命题的是
是两个非零向量,则下列命题为真命题的是 B.若
B.若
 ,则存在实数
,则存在实数 ,使得
,使得



