题目内容
已知圆M:2x2+2y2-8x-8y-1=0和直线l:x+y-9=0过直线l上一点A作△ABC,使∠BAC=45°,AB过圆心M,且B,C在圆M上.(1)当A的横坐标为4时,求直线AC的方程;
(2)求点A的横坐标的取值范围.
分析:(1)根据圆与直线的方程可知:M(2,2),A(4,5),kAM=
,
设直线AC的斜率为k,则有
=1,解得k从而求得直线AC的方程;
(2)将圆的方程化为(x-2)2+(y-2)2=(
)2,设A(a,9-a)①当a≠2时,把∠BAC看作AB到AC的角,又点C在圆M上,由圆心到AC的距离小于等于圆的半径,即
≤
求解.②当a=2时,则A(2,7)与直线x=2成45°角的直线有y-7=x-2,M到它的距离d=
=
>
,这样点C不在圆M上不成立.
| 3 |
| 2 |
设直线AC的斜率为k,则有
|k-
| ||
|1+
|
(2)将圆的方程化为(x-2)2+(y-2)2=(
| ||
| 2 |
| |5×2-2(2a-9)-2a2+22a-81| | ||
|
| ||
| 2 |
| |2-2+5| | ||
|
5
| ||
| 2 |
| ||
| 2 |
解答:解:(1)依题意M(2,2),A(4,5),kAM=
,
设直线AC的斜率为k,则
=1,
解得k=-5或k=
,
故所求直线AC的方程为5x+y-25=0或x-5y+21=0;
(2)圆的方程可化为(x-2)2+(y-2)2=(
)2,设A点的横坐标为a.
则纵坐标为9-a;
①当a≠2时,kAB=
,设AC的斜率为k,把∠BAC看作AB到AC的角,
则可得k=
,直线AC的方程为y-(9-a)=
(x-a)
即5x-(2a-9)y-2a2+22a-81=0,
又点C在圆M上,
所以只需圆心到AC的距离小于等于圆的半径,
即
≤
,
化简得a2-9a+18≤0,
解得3≤a≤6;
②当a=2时,则A(2,7)与直线x=2成45°角的直线为y-7=x-2
即x-y+5=0,M到它的距离d=
=
>
,
这样点C不在圆M上,
还有x+y-9=0,显然也不满足条件,
综上:A点的横坐标范围为[3,6].
| 3 |
| 2 |
设直线AC的斜率为k,则
|k-
| ||
|1+
|
解得k=-5或k=
| 1 |
| 5 |
故所求直线AC的方程为5x+y-25=0或x-5y+21=0;
(2)圆的方程可化为(x-2)2+(y-2)2=(
| ||
| 2 |
则纵坐标为9-a;
①当a≠2时,kAB=
| 7-a |
| a-2 |
则可得k=
| 5 |
| 2a-9 |
| 5 |
| 2a-9 |
即5x-(2a-9)y-2a2+22a-81=0,
又点C在圆M上,
所以只需圆心到AC的距离小于等于圆的半径,
即
| |5×2-2(2a-9)-2a2+22a-81| | ||
|
| ||
| 2 |
化简得a2-9a+18≤0,
解得3≤a≤6;
②当a=2时,则A(2,7)与直线x=2成45°角的直线为y-7=x-2
即x-y+5=0,M到它的距离d=
| |2-2+5| | ||
|
5
| ||
| 2 |
| ||
| 2 |
这样点C不在圆M上,
还有x+y-9=0,显然也不满足条件,
综上:A点的横坐标范围为[3,6].
点评:本题主要考查直线与圆的位置关系及方程的应用,还涉及了直线中的到角公式,点到直线的距离等.

练习册系列答案
相关题目
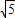 )2+y2=36,定点N(
)2+y2=36,定点N(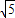 ,0),点P为圆M上的动点,点Q在NP上,点G在MP上,且满足
,0),点P为圆M上的动点,点Q在NP上,点G在MP上,且满足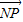 =2
=2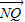 ,
,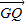 •
•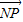 =0.
=0.