题目内容
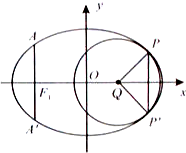 (2013•重庆)如图,椭圆的中心为原点O,长轴在x轴上,离心率e=
(2013•重庆)如图,椭圆的中心为原点O,长轴在x轴上,离心率e=
| ||
| 2 |
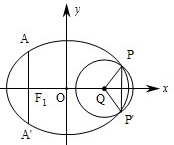
(Ⅰ)求该椭圆的标准方程;
(Ⅱ)取垂直于x轴的直线与椭圆相交于不同的两点P、P′,过P、P′作圆心为Q的圆,使椭圆上的其余点均在圆Q外.若PQ⊥P'Q,求圆Q的标准方程.
分析:(Ⅰ)利用点A(-c,2)在椭圆上,结合椭圆的离心率,求出几何量,即可求得椭圆的标准方程;
(Ⅱ)设出圆Q的圆心坐标及半径,由PQ⊥P'Q得到P的坐标,写出圆的方程后和椭圆联立,化为关于x的二次方程后由判别式等于0得到关于t与r的方程,把P点坐标代入椭圆方程得到关于t与r的另一方程,联立可求出t与r的值,经验证满足椭圆上的其余点均在圆Q外,结合对称性即可求得圆Q的标准方程.
(Ⅱ)设出圆Q的圆心坐标及半径,由PQ⊥P'Q得到P的坐标,写出圆的方程后和椭圆联立,化为关于x的二次方程后由判别式等于0得到关于t与r的方程,把P点坐标代入椭圆方程得到关于t与r的另一方程,联立可求出t与r的值,经验证满足椭圆上的其余点均在圆Q外,结合对称性即可求得圆Q的标准方程.
解答:解:(Ⅰ)由题意知点A(-c,2)在椭圆上,则
+
=1,即
+
=1①
∵离心率e=
,∴
=
=
②
联立①②得:
=
,所以b2=8.
把b2=8代入②得,a2=16.
∴椭圆的标准方程为
+
=1;
(Ⅱ)设Q(t,0),圆Q的半径为r,则圆Q的方程为(x-t)2+y2=r2,
不妨取P为第一象限的点,因为PQ⊥P'Q,则P(t+
r,
r)(t>0).
联立
,得x2-4tx+2t2+16-2r2=0.
由△=(-4t)2-4(2t2+16-2r2)=0,得t2+r2=8
又P(t+
r,
r)在椭圆上,所以
+
=1.
整理得,t=
.
代入t2+r2=8,得
+r2=8.
解得:r2=
.所以t2=
,t=
.
此时t+r=
+
<4.
满足椭圆上的其余点均在圆Q外.
由对称性可知,当t<0时,t=-
,r2=
.
故所求椭圆方程为(x±
)2+y2=
.
| (-c)2 |
| a2 |
| 4 |
| b2 |
| a2-b2 |
| a2 |
| 4 |
| b2 |
∵离心率e=
| ||
| 2 |
| c2 |
| a2 |
| a2-b2 |
| a2 |
| 1 |
| 2 |
联立①②得:
| 4 |
| b2 |
| 1 |
| 2 |
把b2=8代入②得,a2=16.
∴椭圆的标准方程为
| x2 |
| 16 |
| y2 |
| 8 |
(Ⅱ)设Q(t,0),圆Q的半径为r,则圆Q的方程为(x-t)2+y2=r2,
不妨取P为第一象限的点,因为PQ⊥P'Q,则P(t+
| ||
| 2 |
| ||
| 2 |
联立
|
由△=(-4t)2-4(2t2+16-2r2)=0,得t2+r2=8
又P(t+
| ||
| 2 |
| ||
| 2 |
(t+
| ||||
| 16 |
(
| ||||
| 8 |
整理得,t=
8-
| ||
|
代入t2+r2=8,得
(8-
| ||
| 2r2 |
解得:r2=
| 16 |
| 3 |
| 8 |
| 3 |
2
| ||
| 3 |
此时t+r=
2
| ||
| 3 |
4
| ||
| 3 |
满足椭圆上的其余点均在圆Q外.
由对称性可知,当t<0时,t=-
2
| ||
| 3 |
| 16 |
| 3 |
故所求椭圆方程为(x±
2
| ||
| 3 |
| 16 |
| 3 |
点评:本题考查椭圆的标准方程,考查椭圆的几何性质,考查方程组的解法,考查学生的计算能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
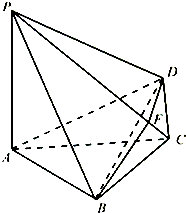 (2013•重庆)如图,四棱锥P-ABCD中,PA⊥底面ABCD,
(2013•重庆)如图,四棱锥P-ABCD中,PA⊥底面ABCD,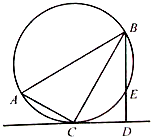 (2013•重庆)如图,在△ABC中,∠C=90°,∠A=60°,AB=20,过C作△ABC的外接圆的切线CD,BD⊥CD,BD与外接圆交于点E,则DE的长为
(2013•重庆)如图,在△ABC中,∠C=90°,∠A=60°,AB=20,过C作△ABC的外接圆的切线CD,BD⊥CD,BD与外接圆交于点E,则DE的长为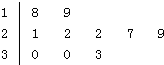 (2013•重庆)如图是某公司10个销售店某月销售某产品数量(单位:台)的茎叶图,则数据落在区间[22,30)内的概率为( )
(2013•重庆)如图是某公司10个销售店某月销售某产品数量(单位:台)的茎叶图,则数据落在区间[22,30)内的概率为( )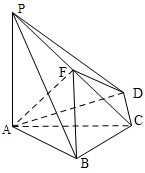 (2013•重庆)如图,四棱锥P-ABCD中,PA⊥底面ABCD,BC=CD=2,AC=4,∠ACB=∠ACD=
(2013•重庆)如图,四棱锥P-ABCD中,PA⊥底面ABCD,BC=CD=2,AC=4,∠ACB=∠ACD=