题目内容
如图，三棱柱A1B1C1―ABC的三视图中，主视图和左视图是全等的矩形，俯视图是等腰直角三角形，已知点M是A1B1的中点.
（1）求证：B1C∥平面AC1M；
（2）设AC与平面AC1M的夹角为θ，求sinθ.
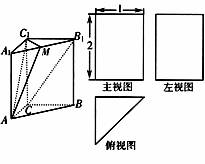
解：由三视图可知三棱柱A1B1C1―ABC为直三棱柱，侧棱长为2，底面是等腰直角三角形，AC=BC=1.
如图建立空间直角坐标系C―xyz，
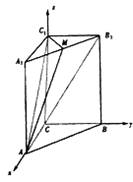
则C（0，0，0），C1（0，0，2），
A（1，0，0），B1（0，1，2），A1（1，0，2）
∵M为A1B1中点，
（1）
∥面AC1M，又∵B1C
面AC1M，
∴B1C∥面AC1M.
（2）设平面AC1M的一个法向量为
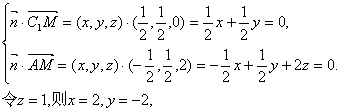
则
练习册系列答案
相关题目
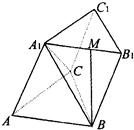如图，三棱柱ABC-A1B1C1的底面是边长为a的正三角形，侧面ABB1A1是菱形且垂直于底面，∠A1AB=60°，M是A1B1的中点．
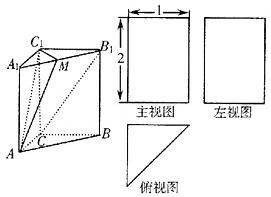如图，三棱柱A1B1C1-ABC的三视图中，主视图和左视图是全等的矩形，俯视图是等腰直角三角形，已知点M式A1B1的中点．
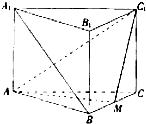如图，三棱柱ABC-A1B1C1中，侧棱与底面垂直，AB=BC=2AA1，∠ABC=90°，M是BC中点．
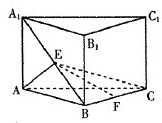如图，三棱柱ABC-A1B1 C1中，侧棱AA1⊥平面ABC，AB=BC=AA1=2，AC=2
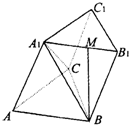如图，三棱柱ABC-A1B1C1的底面是边长为a的正三角形，侧面ABB1A1是菱形且垂直于底面，∠A1AB=60°，M是A1B1的中点．