题目内容
（A）在极坐标系中，曲线C1：ρ=2cosθ，曲线C2：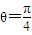
，若曲线C1与C2交于A、B两点，则线段AB= ．（B）若|x-1|+x-2||+|x-3|≥m恒成立，则m的取值范围为 ．
【答案】分析：（A）直接代入
，求出ρ的值，就是线段AB的长．
（B）求出|x-1|+x-2||+|x-3|的最小值，即可求出m的范围．
解答：解：（A）在极坐标系中，曲线C1：ρ=2cosθ，曲线C2：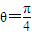
，曲线C1与C2交于A、B两点，其中一点是坐标原点，所以|AB|=2cos
=
；
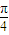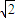（B）由绝对值的几何意义可知|x-1|+x-2||+|x-3|的最小值为：2；要|x-1|+x-2||+|x-3|≥m恒成立，所以m≤2；
故答案为：（A）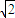
；（B）m≤2
点评：本题是基础题，（A）考查极坐标方程的应用，极径的求法；（B）考查绝对值的几何意义，恒成立问题的应用，考查计算能力，转化思想的应用．
，求出ρ的值，就是线段AB的长．（B）求出|x-1|+x-2||+|x-3|的最小值，即可求出m的范围．
解答：解：（A）在极坐标系中，曲线C1：ρ=2cosθ，曲线C2：
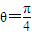，曲线C1与C2交于A、B两点，其中一点是坐标原点，所以|AB|=2cos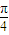=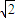；（B）由绝对值的几何意义可知|x-1|+x-2||+|x-3|的最小值为：2；要|x-1|+x-2||+|x-3|≥m恒成立，所以m≤2；
故答案为：（A）
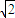；（B）m≤2点评：本题是基础题，（A）考查极坐标方程的应用，极径的求法；（B）考查绝对值的几何意义，恒成立问题的应用，考查计算能力，转化思想的应用．
练习册系列答案
小学夺冠AB卷系列答案
ABC考王全优卷系列答案
相关题目
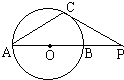C．如图⊙o的直径AB=6cm，P是AB的延长线上一点，过点P作⊙o的切线，切点为C，连接AC，若∠CPA=30°，则PC=