题目内容
选做题(请考生在两个小题中任选一题作答,如果多做,则按所做的第一题评阅记分).
(A)在极坐标系中,过圆ρ=6cosθ的圆心,且垂直于极轴的直线的极坐标方程是
(B) 当x,y满足条件|x-1|+|y+1|<1时,变量μ=
的取值范围是
(A)在极坐标系中,过圆ρ=6cosθ的圆心,且垂直于极轴的直线的极坐标方程是
ρcosθ=3
ρcosθ=3
.(B) 当x,y满足条件|x-1|+|y+1|<1时,变量μ=
| x-1 |
| y-2 |
(-
,
)
| 1 |
| 3 |
| 1 |
| 3 |
(-
,
)
.| 1 |
| 3 |
| 1 |
| 3 |
分析:(A)直接求出圆的直角坐标方程,求出圆心坐标,然后求出所求直线方程;
(B)画出绝对值不等式表示的可行域,利用
的几何意义,求出取值范围.
(B)画出绝对值不等式表示的可行域,利用
| x-1 |
| y-2 |
解答: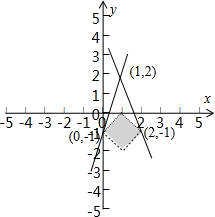 解:(A)在极坐标系中,圆ρ=6cosθ,即x2+y2-6x=0,
解:(A)在极坐标系中,圆ρ=6cosθ,即x2+y2-6x=0,
所以圆的圆心(3,0)半径为3,
所以过圆ρ=6cosθ的圆心,且垂直于极轴的直线的极坐标方程是ρcosθ=3.
(B)|x-1|+|y+1|<1在直角坐标系中的可行域如图:
变量μ=
的几何意义是可行域内的点与(1,2)点连线的斜率的倒数的范围.
所以
∈(-∞,-3)∪(3,+∞),所以
∈(-
,
).
故答案为:(-
,
).
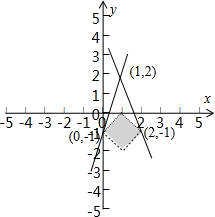 解:(A)在极坐标系中,圆ρ=6cosθ,即x2+y2-6x=0,
解:(A)在极坐标系中,圆ρ=6cosθ,即x2+y2-6x=0,所以圆的圆心(3,0)半径为3,
所以过圆ρ=6cosθ的圆心,且垂直于极轴的直线的极坐标方程是ρcosθ=3.
(B)|x-1|+|y+1|<1在直角坐标系中的可行域如图:
变量μ=
| x-1 |
| y-2 |
所以
| y-1 |
| x-1 |
| x-1 |
| y-2 |
| 1 |
| 3 |
| 1 |
| 3 |
故答案为:(-
| 1 |
| 3 |
| 1 |
| 3 |
点评:本题考查绝对值不等式,简单线性规划,简单曲线的极坐标方程,考查计算能力.

练习册系列答案
相关题目
 的圆心,且垂直于极轴的直线的极坐标方程是
的圆心,且垂直于极轴的直线的极坐标方程是
 的圆心,且垂直于极轴的直线的极坐标方程为 .
的圆心,且垂直于极轴的直线的极坐标方程为 .