题目内容
从10名大学生中选3个人担任乡村干部,则甲、丙至少有1人入选,而乙没有入选的不同选法的种数为 ( )
| A. 85 | B. 56 | C. 49 | D. 28 |
C
解析试题分析:若甲、丙有1人入选,则不同的选法总数为 种;若甲、丙都入选,则不同的选法总数为
种;若甲、丙都入选,则不同的选法总数为 种,所以不同的选法总数共有
种,所以不同的选法总数共有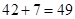 种.
种.
考点:本小题主要考查分类加法计数原理和分步乘法计数原理的综合应用,考查学生运用数学知识解决实际问题的能力.
点评:在解决这类问题时,要分清楚是需要分类还是需要分步,如果都需要,则一般是先分类后分步.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
若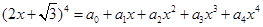 ,则
,则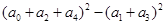 的值为
的值为
A.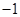 | B.1( | C.2 | D.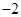 |
下列排列数中,等于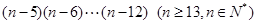 的是( )
的是( )
A.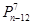 | B.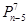 | C.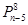 | D.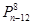 |
若(x+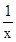 )n展开式的二项式系数之和为64,则展开式的常数项为( )
)n展开式的二项式系数之和为64,则展开式的常数项为( )
| A.10 | B.20 | C.30 | D.120 |
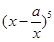 的展开式中x3的系数为10,则实数a为
的展开式中x3的系数为10,则实数a为
| A.-2 | B.-1 | C. 1 | D. 2 |
从6名志愿者中选出4人分别从事翻译、导游、导购、保洁四项不同的工作,若其中甲、乙两名志愿者不能从事翻译工作,则选派方案共有 ( )
| A.280种 | B.240种 | C.180种 | D.96种 |
用数字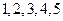 组成无重复数字的五位数,则
组成无重复数字的五位数,则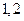 相邻,而
相邻,而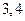 不相邻的数有( )
不相邻的数有( )
| A.12个 | B.24个  | C.36个 | D.48个 |
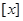 表示不超过
表示不超过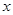 的最大整数(如
的最大整数(如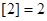 ,
,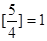 ),对于给定的
),对于给定的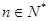 ,定义
,定义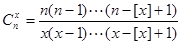 ,
,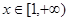 ,则当
,则当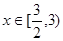 时,函数
时,函数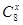 的值域是( )
的值域是( )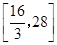

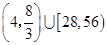
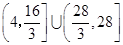
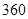 种
种 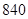 种
种 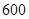 种
种 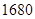 种
种