若函数$f(x)=\frac{1}{a}{x^2}-2ax+5$在区间上单调递增.在区间上单调递减.则a=( )A．1B．-1C．±1D．不存在题目和参考答案——青夏教育精英家教网—

题目内容

7．若函数$f（x）=\frac{1}{a}{x^2}-2ax+5$在区间（-∞，1）上单调递增，在区间（1，+∞）上单调递减，则a=（　　）

A．

B．

-1

C．

±1

D．

不存在

分析由题意得到f（x）的对称轴为x=1，且a＜0，再根据对称轴公式代值求出a的值．

解答解：∵函数$f（x）=\frac{1}{a}{x^2}-2ax+5$在区间（-∞，1）上单调递增，在区间（1，+∞）上单调递减，
∴函数f（x）的对称轴为x=1=$\frac{2a}{2•\frac{1}{a}}$，且a＜0，
解的a=-1，
故选：B．

点评本题考查二次函数图象特征和单调性，以及不等式的解法，属于基础题．

练习册系列答案

中考研究全国各省市中考真题常考基础题系列答案

相关题目

17．

直三棱柱ABC-A₁B₁C₁中，D，E分别是AB，BB₁点的中点，且AA₁=AC=BC=$\frac{\sqrt{2}}{2}$AB．
（1）证明：BC₁∥平面A₁CD；
（2）求直线CE与平面A₁CD所成角的正弦值．

18．如图，在复平面内，复数z₁和z₂对应的点分别是A和B，则$\frac{{z}_{2}}{{z}_{1}}$=（　　）

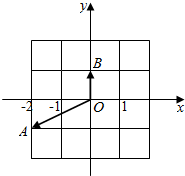
A．

$\frac{1}{5}$+$\frac{2}{5}$i

B．

$\frac{2}{5}$+$\frac{1}{5}$i

C．

-$\frac{1}{5}$-$\frac{2}{5}$i

D．

-$\frac{2}{5}$-$\frac{1}{5}$i

15．已知椭圆E的中心在坐标原点O，焦点在坐标轴上，且经过M（2，1），N（2$\sqrt{2}$，0）两点．
（1）求椭圆E的方程；
（2）若平行于OM的直线l交椭圆E于两个不同点A，B，直线MA与MB的斜率分别为k₁，k₂，试问：k₁+k₂是否为定值？若是，求出此定值；若不是，说明理由．

2．已知关于x的x²-2ax+a+2=0的两个实数根是α，β，且有1＜α＜2＜β＜3，则实数a的取值范围是$（{2，\frac{11}{5}}）$．

12．已知全集U=R，A={x|-4≤x≤2}，B={x|-1＜x≤3}，P={x|x≤0，或x≥$\frac{5}{2}$}，Q={x|a-2＜x＜a+2}．
（1）求A∩B；
（2）求（∁_UB）∪P；
（3）若A∩B⊆Q，求实数a的取值范围．

19．

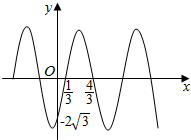已知函数f（x）=Asin（ωx+φ）（ω＞0，-π＜φ＜0）的部分图象如图所示，则下列判断错误的是（　　）

	A．	函数f（x）的最小正周期为2
	B．	函数f（x）的值域为[一4，4]
	C．	函数f（x）的图象关于（ $\frac{10}{3}$，0）对称
	D．	函数f（x）的图象向左平移 $\frac{π}{3}$个单位后得到y=Asinωx的图象

16．用导数的定义，求函数y=$\frac{1}{{x}^{2}}$+2在x=1处的导数．

试题分类