题目内容
9.某位同学进行寒假社会实践活动,为了对白天平均气温与某奶茶店的某种饮料销量之间的关系进行分析研究,他分别记录了1月11日至1月15日的白天平均气温x(℃)与该小卖部的这种饮料销量y(杯),得到如下数据:| 日期 | 1月11日 | 1月12日 | 1月13日 | 1月14日 | 1月15日 |
| 平均气温x( ) | 9 | 10 | 12 | 11 | 8 |
| 销量y(杯) | 23 | 25 | 30 | 26 | 21 |
(2)请根据所给五组数据,求出y关于x的线性回归方程y=bx+a;并根据线性回归方程预测当天气预报1月16日的白天平均气温7(℃)时奶茶店这种饮料的销量.
分析 (1)根据题意列举出从5组数据中选取2组数据共有10种情况,每种情况都是可能出现的,满足条件的事件包括的基本事件有4种.根据等可能事件的概率做出结果.
(2)根据所给的数据,先做出x,y的平均数,即做出本组数据的样本中心点,根据最小二乘法求出线性回归方程的系数,写出线性回归方程.利用线性回归方程,x取7,即可预测该奶茶店这种饮料的销量.
解答 解:(1)设“选取的2组数据恰好是相邻2天数据”为事件A,∵所有基本事件(m,n)(其中m,n为1月份的日期数)有:(11,12),(11,13),(11,14),(11,15),(12,13),(12,14),(12,15),(13,14),(13,15),(14,15),共有10种. …(2分)
事件A包括的基本事件有(11,12),(12,13),(13,14),(14,15)共4种.…(2分)
∴抽出的2组数据恰好是相邻2天数据的概率P(A)=$\frac{4}{10}$=$\frac{2}{5}$ …(1分)
(2)∵$\overline{x}$=$\frac{9+10+12+11+8}{5}=10$,…(1分)(6分)
$\overline{y}$=$\frac{23+25+30+26+21}{5}$=25.…(1分)(7分)
∴由公式,求得$\hat{b}$=2.1,a=$\overline{y}-\widehat{b}\overline{x}$=4 …(2分)
∴y关于x的线性回归方程为:$\hat{y}$=2.1x+4 …(1分)
∵当x=7时,$\hat{y}$=2.1×7+4=18.7,…(1分)
∴该奶茶店这种饮料的销量大约为19杯(或18杯).…(1分)
点评 本题考查等可能事件的概率,考查线性回归方程的求法,考查最小二乘法,考查估计验算所求的方程是否是可靠的,是一个综合题目.

| A. | $\frac{\sqrt{2}}{2}$ | B. | -$\frac{\sqrt{2}}{2}$ | C. | $\frac{\sqrt{5}}{5}$ | D. | -$\frac{\sqrt{5}}{5}$ |
| A. | 4$\sqrt{3}$-$\frac{π}{6}$ | B. | 4$\sqrt{3}$-$\frac{π}{3}$ | C. | $\frac{π}{2}$ | D. | $\frac{\sqrt{3}}{4}$+$\frac{π}{6}$ |
| A. | M>N>P | B. | P<M<N | C. | N>P>M |
| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | $\frac{3}{4}$ | D. | $\frac{1}{3}$ |
| A. | (-$\frac{3π}{8}+kπ,\frac{π}{8}+kπ$)k∈Z | B. | (-$\frac{3π}{8}+\frac{kπ}{2},\frac{π}{8}+\frac{kπ}{2}$)k∈Z | ||
| C. | ($\frac{π}{8}+kπ,\frac{5π}{8}+kπ$)k∈Z | D. | (-$\frac{3π}{8}+2kπ,\frac{π}{8}+2kπ$)k∈Z |
 中,内角
中,内角 的对边分别为
的对边分别为 ,已知
,已知 .
. 的大小;
的大小; ,且
,且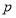 的取值范围.
的取值范围.