题目内容
用平面α截半径为R的球,如果球心到截面的距离为| R | 2 |
分析:利用球的半径,球心到截面的距离,求出小圆半径,再求小圆面积;进而可求出球的表面积,然后可得比值.
解答:解:小圆半径是:
R,小圆的面积是:
R2,
球的表面积是;4πR2
截得小圆的面积与球的表面积的比值为:
R2:4πR2=3:16
故答案为:3:16
| ||
| 2 |
| 3π |
| 4 |
球的表面积是;4πR2
截得小圆的面积与球的表面积的比值为:
| 3π |
| 4 |
故答案为:3:16
点评:本题考查球的表面积,球的截面面积,是基础题.

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
 ,
, .两截面间的距离d=27cm求R.
.两截面间的距离d=27cm求R. ,
, ,两截面间的距离为d=27cm,求球的表面积.
,两截面间的距离为d=27cm,求球的表面积. ,
,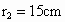 .两截面间的距离d=27cm求R.
.两截面间的距离d=27cm求R. ,
, ,两截面间的距离为d=27cm,求球的表面积.
,两截面间的距离为d=27cm,求球的表面积.