题目内容
设函数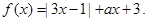
(1)若a=1,解不等式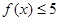 ;
;
(2)若函数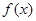 有最小值,求实数a的取值范围。
有最小值,求实数a的取值范围。
【答案】
(Ⅰ)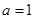 时,
时,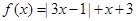 .
.
当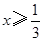 时,
时,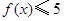 可化为
可化为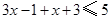 ,解之得
,解之得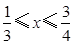 ;
;
当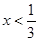 时,
时,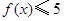 可化为
可化为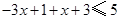 ,解之得
,解之得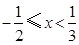 .
.
综上可得,原不等式的解集为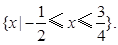
(Ⅱ)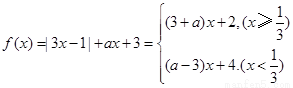
函数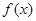 有最小值的充要条件为
有最小值的充要条件为 即
即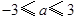
【解析】略

练习册系列答案
 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目
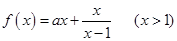
 的最小值;
的最小值;
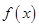 的最小值;
的最小值;