题目内容
已知直线 :
: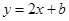 与函数
与函数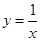 的图象交于
的图象交于 ,
, 两点,记△
两点,记△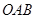 的面积为
的面积为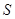 (
(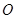 为坐标原点),则函数
为坐标原点),则函数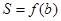 是( )
是( )
A.奇函数且在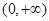 上单调递增 上单调递增 |
B.偶函数且在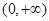 上单调递增 上单调递增 |
C.奇函数且在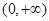 上单调递减 上单调递减 |
D.偶函数且在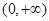 上单调递减 上单调递减 |
B
解析试题分析:由题意,如下图: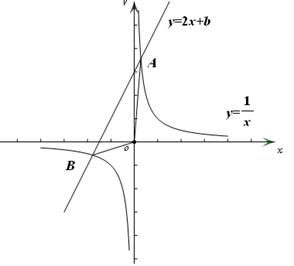
设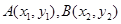 ,联立
,联立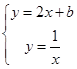 得
得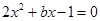 ,则
,则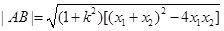
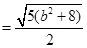 ,
, 点到直线
点到直线 的距离
的距离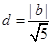 ,∴
,∴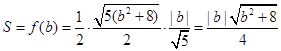 .
.
∵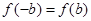 ,∴
,∴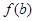 为偶函数.当
为偶函数.当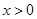 时,
时,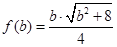 ,易知
,易知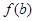 单调递增.故选B.
单调递增.故选B.
考点:1.函数奇偶性;2.三角形面积应用.

练习册系列答案
相关题目
函数 在定义域内零点的个数为( )
在定义域内零点的个数为( )
| A.0 | B.1 | C.2 | D.3 |
已知偶函数 满足
满足 ,且当
,且当 时,
时, ,则关于
,则关于 的方程
的方程 在
在 上根的个数是( )
上根的个数是( )
A. 个 个 | B. 个 个 | C. 个 个 | D. |
下列说法正确的是( )
A.命题“存在 , , ”的否定是“任意 ”的否定是“任意 , , ” ” |
| B.两个三角形全等是这两个三角形面积相等的必要条件 |
C.函数 在其定义域上是减函数 在其定义域上是减函数 |
D.给定命题 ,若“ ,若“ 且 且 ”是真命题,则 ”是真命题,则 是假命题 是假命题 |
设f(x)为定义在R上的奇函数,当x≥0时,f(x)=2x+2x+b(b为常数),则f(﹣1)=( )
| A.﹣3 | B.﹣1 | C.1 | D.3 |
已知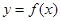 是定义在R上的偶函数,且在[0,+
是定义在R上的偶函数,且在[0,+ )上单调递增,则满足f(m)<f(1)的实数m的范围是
)上单调递增,则满足f(m)<f(1)的实数m的范围是
A.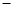 l<m<0 l<m<0 |
| B.0<m<1 |
C.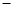 l<m<1 l<m<1 |
D.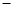 l≤m≤1 l≤m≤1 |
设动直线 与函数
与函数 的图象分别交于点M、N,则|MN|的最小值为( )
的图象分别交于点M、N,则|MN|的最小值为( )
A. |
B. |
C. |
D. |
函数 的定义域是( )
的定义域是( )
A. |
B. |
C. |
D. |
