题目内容
17.已知函数f(x)=$\frac{{2}^{x}-a}{{2}^{x}+b}$为定义在R上的奇函数.(1)求a,b的值及f(x)的表达式;
(2)判断f(x)在定义域上的单调性并用单调性的定义证明.
分析 (1)根据题意,由于函数f(x)是定义在R上的奇函数,则有f(0)=0,f(1)=-f(-1),代入数据,计算可得a、b的值;
(2)首先对f(x)的表达式变形可得f(x)=1-$\frac{2}{{2}^{x}+1}$,用作差法判断函数单调性即可.
解答 解:(1)∵f(x)=$\frac{{2}^{x}-a}{{2}^{x}+b}$定义在R上的奇函数,
则有f(0)=0,即$\frac{1-a}{1+b}$=0,解可得a=1;
又f(1)=-f(-1),即$\frac{2-a}{2+b}$=-$\frac{\frac{1}{2}-1}{\frac{1}{2}+b}$,解可得b=1.
∴f(x)=$\frac{{2}^{x}-1}{{2}^{x}+1}$;
(2)由(1)可得,f(x)=1-$\frac{2}{{2}^{x}+1}$
设x1<x2,
则f(x1)-f(x2)=$\frac{2({2}^{{x}_{1}}-{2}^{{x}_{2}})}{({2}^{{x}_{1}}+1)({2}^{{x}_{2}}+1)}$,
∵x1<x2,
∴${2}^{{x}_{1}}-{2}^{{x}_{2}}$<0,
∴f(x1)-f(x2)<0,
∴f(x)是增函数.
点评 本题考查函数的单调性、奇偶性,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目
8.如果loga2>logb2>0,那么( )
| A. | 1<a<b | B. | 1<b<a | C. | 0<a<b<1 | D. | 0<b<a<1 |
5.定义在R上的偶函数f(x)满足f(x+1)=-f(x),且在[0,1]上单调递增,设a=f(3),b=f($\sqrt{2}$),c=f(2),则a,b,c大小关系是( )
| A. | b>c>a | B. | a>c>b | C. | a>b>c | D. | c>b>a |
5.执行下面框图,则输出m的结果是( )


| A. | 5 | B. | 7 | C. | 9 | D. | 11 |

 满足:①
满足:① ;②
;②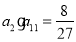 ;③
;③ .
. ,问:是否存在常数
,问:是否存在常数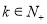 ,使得
,使得 对于任意
对于任意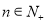 恒成立?若存在,请求出
恒成立?若存在,请求出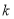 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.