题目内容
在数列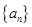 中,
中,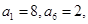 且满足
且满足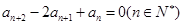 .
.
(1)求数列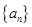 的通项公式;(2)设
的通项公式;(2)设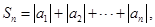 求
求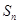 .
.
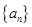 中,
中,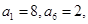 且满足
且满足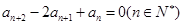 .
.(1)求数列
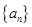 的通项公式;(2)设
的通项公式;(2)设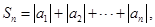 求
求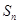 .
.(1)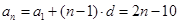 .(2)
.(2)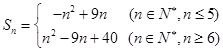
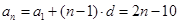 .(2)
.(2)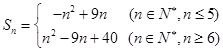
本试题主要是考查了等差数列的通项公式的运用,以及数列求和的综合运用。
(1)因为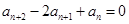 ,则
,则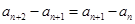
所以数列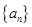 是等差数列,设其公差为
是等差数列,设其公差为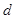 .
.
由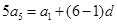 ,得
,得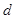 =2从而得到通项公式。
=2从而得到通项公式。
(2)由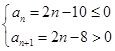 ,得
,得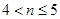 .
.
所以当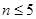 时,
时,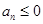 ;当
;当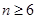 时,
时,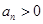 .
.
因此要分类讨论得到结论。
解:(1)因为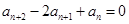 ,则
,则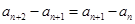
所以数列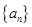 是等差数列,设其公差为
是等差数列,设其公差为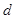 .
.
由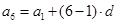 ,得
,得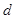 =2.
=2.
又因为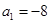 ,所以数列
,所以数列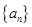 的通项公式为
的通项公式为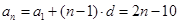 .
.
(2)由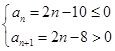 ,得
,得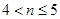 .
.
所以当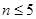 时,
时,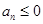 ;当
;当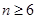 时,
时,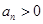 .
.
当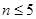 时,
时, =
=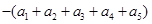 =
= ;
;
当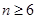 时,
时,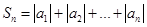 =
=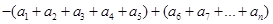
=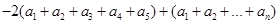
=40+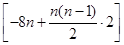 =
=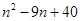 .
.
所以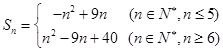
(1)因为
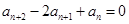 ,则
,则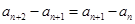
所以数列
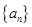 是等差数列,设其公差为
是等差数列,设其公差为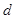 .
.由
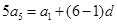 ,得
,得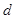 =2从而得到通项公式。
=2从而得到通项公式。(2)由
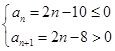 ,得
,得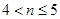 .
.所以当
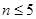 时,
时,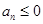 ;当
;当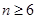 时,
时,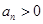 .
.因此要分类讨论得到结论。
解:(1)因为
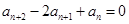 ,则
,则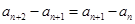
所以数列
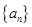 是等差数列,设其公差为
是等差数列,设其公差为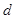 .
.由
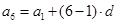 ,得
,得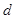 =2.
=2. 又因为
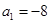 ,所以数列
,所以数列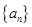 的通项公式为
的通项公式为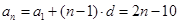 .
.(2)由
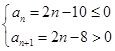 ,得
,得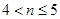 .
.所以当
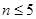 时,
时,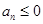 ;当
;当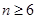 时,
时,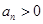 .
.当
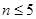 时,
时, =
=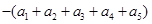 =
= ;
;当
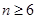 时,
时,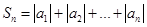 =
=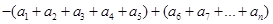
=
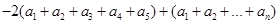
=40+
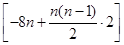 =
=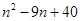 .
.所以
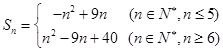

练习册系列答案
相关题目
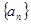 满足
满足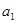 =-1,
=-1,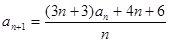 ,数列
,数列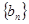 满足
满足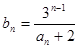
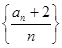 为等比数列,并求数列
为等比数列,并求数列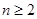 时,
时,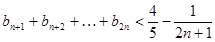
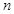 项和为
项和为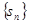 ,求证:当
,求证:当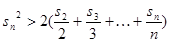 .
.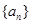 满足如图所示的程序框图。
满足如图所示的程序框图。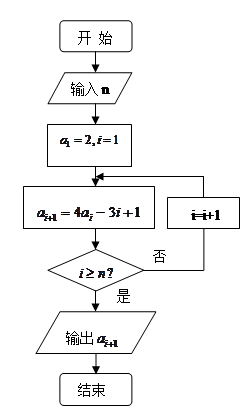
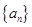 的通项公式
的通项公式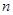 项和
项和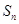 ,证明不等式
,证明不等式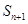 ≤
≤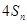 ,对任意
,对任意 皆成立.
皆成立.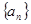 的前
的前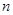 项和为
项和为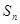 ,且
,且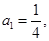
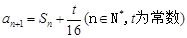 .
.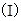 若数列
若数列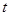 的值;
的值;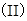 若
若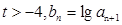 ,数列
,数列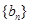 前
前 ,
,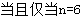 时
时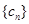 ,其中
,其中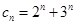 ,且数列
,且数列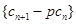 为等比数列,求常数p;
为等比数列,求常数p;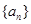 、
、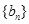 是公比不相等的两个等比数列,
是公比不相等的两个等比数列,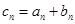 ,证明:数列
,证明:数列 的前
的前 项和为
项和为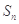 ,等比数列
,等比数列 的各项均为正数,公比是
的各项均为正数,公比是 ,且满足:
,且满足: .
.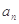 与
与 ;
; ,若
,若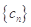 满足:
满足: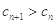 对任意的
对任意的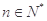 恒成立,求
恒成立,求 的取值范围.
的取值范围. 中,
中, ,
, ,则
,则 等于
等于 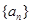 、
、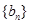 的前
的前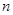 项和的比
项和的比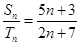 ,则
,则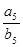 的值是 .
的值是 .