题目内容
1.数列{an}满足an+1=$\frac{1}{{1-a}_{n}}$,a8=2,则a1=$\frac{1}{2}$.分析 把已知递推式变形为${a}_{n}=1-\frac{1}{{a}_{n+1}}$,然后结合a8=2逐一求出数列前7项,则a1可求.
解答 解:由an+1=$\frac{1}{{1-a}_{n}}$,得${a}_{n}=1-\frac{1}{{a}_{n+1}}$,
又a8=2,
∴${a}_{7}=1-\frac{1}{{a}_{8}}=\frac{1}{2}$,${a}_{6}=1-\frac{1}{{a}_{7}}=-1$,
${a}_{5}=1-\frac{1}{{a}_{6}}=2$,${a}_{4}=1-\frac{1}{{a}_{5}}=\frac{1}{2}$,
${a}_{3}=1-\frac{1}{{a}_{4}}=-1$,${a}_{2}=1-\frac{1}{{a}_{3}}=2$,${a}_{1}=1-\frac{1}{{a}_{2}}=\frac{1}{2}$.
故答案为:$\frac{1}{2}$.
点评 本题考查了数列递推式,考查了学生的运算能力,是基础题.

练习册系列答案
相关题目
13.设复数z1=l+2i,z2=l-ai,若z1•z2为实数,则实数a=( )
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
10.已知集合P={0,1,2},Q={y|y=3x},则P∩Q=( )
| A. | {0,1} | B. | {1,2} | C. | {0,1,2} | D. | ∅ |
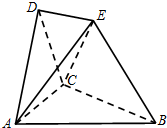 如图,在空间几何体ABCDE中,平面ACD⊥平面ABC,△ABC和△ACD都是边长为2的等边三角形,BE=2,点E在平面ABC内的射影落在∠ABC的平分线上,若DE∥平面ABC.
如图,在空间几何体ABCDE中,平面ACD⊥平面ABC,△ABC和△ACD都是边长为2的等边三角形,BE=2,点E在平面ABC内的射影落在∠ABC的平分线上,若DE∥平面ABC.