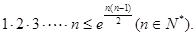题目内容
已知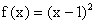 ,
,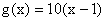 ,数列
,数列 满足
满足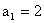 ,
,
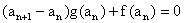 ,
, 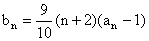 .
.
(I)求证:数列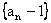 是等比数列;
是等比数列;
(II)当n取何值时,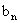 取最大值,并求出最大值;
取最大值,并求出最大值;
(III)若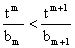 对任意
对任意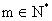 恒成立,求实数
恒成立,求实数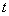 的取值范围.
的取值范围.
【答案】
解:(I)∵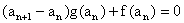 ,
,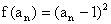 ,
,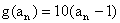 ,
,
∴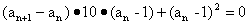 .
.
即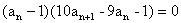 .…………………………………………1分
.…………………………………………1分
又若an≠1,则an+1≠1,事实上当an≠1时,由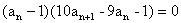 知
知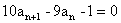 ,若an+1=1,则an=1,从而与an≠1矛盾,故an+1≠1.
,若an+1=1,则an=1,从而与an≠1矛盾,故an+1≠1.
由此及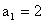 ≠1可知an≠1对任意n∈N
≠1可知an≠1对任意n∈N 都成立.
都成立.
故对任何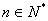 ,
,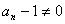 ,………………………………………3分
,………………………………………3分
所以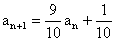 .
.
∵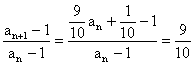 ,
,
∴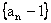 是以
是以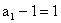 为首项,
为首项,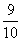 为公比的等比数列.…………5分
为公比的等比数列.…………5分
(II)由(I)可知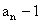 =
=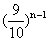 (
( ).
).
∴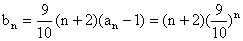 .
.

(III)由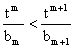 ,得
,得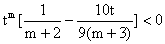 ……………… (*)
……………… (*)
依题意(*)式对任意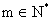 恒成立,
恒成立,
①当t=0时,(*)式显然不成立,因此t=0不符合题意.…………10分
②当t<0时,由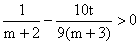 ,可知
,可知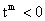 (
(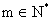 ).
).
而当m是偶数时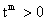 ,因此t<0不符合题意.………………11分
,因此t<0不符合题意.………………11分
③当t>0时,由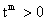 (
(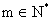 ),
),
∴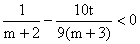 ,∴
,∴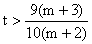 .(
.(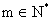 )
)
设 (
(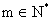 ),
),
∵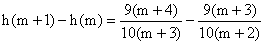 =
=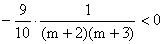 ,
,
∴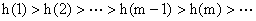 .
.
∴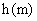 的最大值为
的最大值为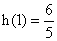 .………………………………13分
.………………………………13分
所以实数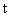 的取值范围是
的取值范围是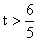 .………………………………14分
.………………………………14分

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
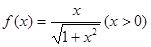 ,数列
,数列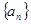 满足
满足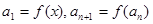 。
。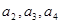 ;
;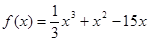 ,数列
,数列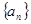 满足
满足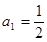 ,
,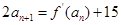 ;数列
;数列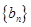 的前
的前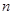 项和为
项和为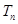 ,数列
,数列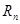 ,
,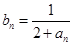
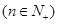 .
.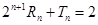 ;
;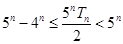 .
. 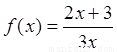 ,数列
,数列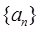 满足
满足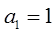 ,
,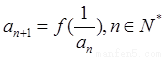 .
.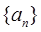 的通项公式;
的通项公式; 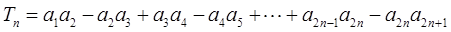 ,求
,求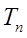 ;
;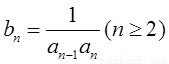 ,
,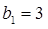 ,
,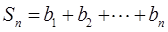 ,若
,若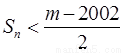 对一切
对一切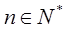 成立,求最小正整数
成立,求最小正整数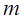 .
.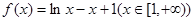 ,数列
,数列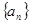 满足
满足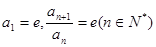 .
.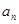 ;
;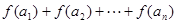 ;
;