关于x的方程x2-kx+(k+3)=0的解都是正数.求实数k的取值范围．题目和参考答案——青夏教育精英家教网—

题目内容

9．关于x的方程x²-kx+（k+3）=0的解都是正数，求实数k的取值范围．

分析由条件利用一元二次方程根的分布与系数的关系，二次函数的性质求得实数k的取值范围．

解答解：关于x的方程x²-kx+（k+3）=0的解都是正数，∴$\left\{\begin{array}{l}{△{=k}^{2}-4（k+3）≥0}\\{{x}_{1}{+x}_{2}=k＞0}\\{{x}_{1}{•x}_{2}=k+3＞0}\end{array}\right.$，
求得k≥6．

点评本题主要考查一元二次方程根的分布与系数的关系，二次函数的性质，体现了转化的数学思想，属于基础题．

练习册系列答案

20．若正实数a，b，c满足3a²+10ab-8b²=c²，且a＞b，若不等式5a+6b≥kc恒成立，则实数k的最大值为2．

17．已知实数x，y满足$\left\{\begin{array}{l}{x-y+1≥0}\\{x+2y+1≥0}\\{3x-y-3≤0}\end{array}\right.$，则|x-2y-1|的取值范围是[0，$\frac{10}{7}$]．

4．

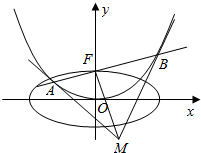已知抛物线C：x²=2py（p＞0）的焦点为F（0，1），过点F作直线l交抛物线C于A，B两点．椭圆E的中心在原点，焦点在x轴上，点F是它的一个顶点，且其离心率$e=\frac{{\sqrt{3}}}{2}$．
（Ⅰ）分别求抛物线C和椭圆E的方程；
（Ⅱ）经过A，B两点分别作抛物线C的切线l₁，l₂，切线l₁与l₂相交于点M．证明AB⊥MF．

14．不等式mx²+mx-2＜0的解集为R，则实数m的取值范围为（-8，0]．

1．求证：函数$f（x）=\frac{1}{x}+1$在（0，+∞）上是减函数．

18．已知f（x）=x²-ax+1在[b，b+2]上是偶函数，则f（x）的递增区间是[0，1]．

19．已知f（x）=x²+2x+3≥ax，（x＞0），求a的取值范围．

试题分类