题目内容
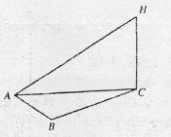
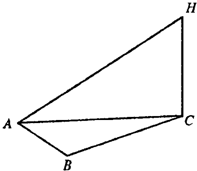
某气象仪器研究所按以下方案测试一种“弹射型”气象观测仪器的垂直弹射高度:在C处进行该仪器的垂直弹射,观察点A、B两地相距100m,∠BAC=60°,在A地听到弹射声音的时间比B地晚
s.A地测得该仪器在C处时的俯角为15°,A地测得最高点H的仰角为30°,求该仪器的垂直弹射高度CH.(声音的传播速度为340m/s)
| 2 | 17 |
分析:根据题意画出相应的图形,过A作AD垂直于CH,设|AC|=x,根据在A地听到弹射声音的时间比B地晚
s,由声音的速度表示出|BC|,在三角形ABC中,由余弦定理列出关于x的方程,求出方程的解得到x的值,确定出|AC|的长,再三角形ACH中,利用正弦定理求出|CH|的长即可.
| 2 |
| 17 |
解答: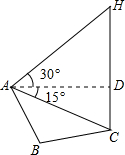 解:根据题意画出图形,过A作AD⊥CH,如图所示,
解:根据题意画出图形,过A作AD⊥CH,如图所示,
设|AC|=x,根据题意得:|BC|=x-
×340=x-40,
在△ABC内,由余弦定理得:|BC|2=|BA|2+|CA|2-2|BA|•|CA|•cos∠BAC,
即(x-40)2=x2+10000-100x,解得x=420,
在△ACH中,|AC|=420,∠CAH=30°+15°=45°,∠CHA=90°-30°=60°,
由正弦定理:
=
,得|CH|=|AC|•
=140
,
答:该仪器的垂直弹射高度CH为140
m.
 解:根据题意画出图形,过A作AD⊥CH,如图所示,
解:根据题意画出图形,过A作AD⊥CH,如图所示,设|AC|=x,根据题意得:|BC|=x-
| 2 |
| 17 |
在△ABC内,由余弦定理得:|BC|2=|BA|2+|CA|2-2|BA|•|CA|•cos∠BAC,
即(x-40)2=x2+10000-100x,解得x=420,
在△ACH中,|AC|=420,∠CAH=30°+15°=45°,∠CHA=90°-30°=60°,
由正弦定理:
| |CH| |
| sin∠CAH |
| |AC| |
| sin∠AHC |
| sin∠CAH |
| sin∠AHC |
| 6 |
答:该仪器的垂直弹射高度CH为140
| 6 |
点评:此题考查了正弦、余弦定理,以及特殊角的三角函数值,根据题意画出相应的图形是解本题的关键.

练习册系列答案
相关题目
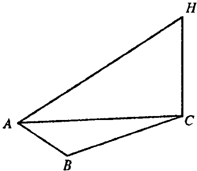 某气象仪器研究所按以下方案测试一种“弹射型”气象观测仪器的垂直弹射高度:A、B、C三地位于同一水平面上,在C处进行该仪器的垂直弹射,观测点A、B两地相距100米,∠BAC=60°,在A地听到弹射声音的时间比B地晚
某气象仪器研究所按以下方案测试一种“弹射型”气象观测仪器的垂直弹射高度:A、B、C三地位于同一水平面上,在C处进行该仪器的垂直弹射,观测点A、B两地相距100米,∠BAC=60°,在A地听到弹射声音的时间比B地晚 ,在A地听到弹射声音的时间比B地晚
,在A地听到弹射声音的时间比B地晚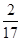 秒,A地测得该仪器在C处时的俯角为15°A地测得最高点H时的仰角为30°,求该仪器的垂直弹射高度CH(声音的传播速度为340米/秒)
秒,A地测得该仪器在C处时的俯角为15°A地测得最高点H时的仰角为30°,求该仪器的垂直弹射高度CH(声音的传播速度为340米/秒)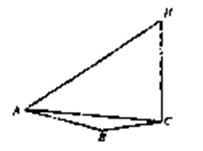
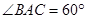 ,在A地听到弹射声音的时间比B地晚
,在A地听到弹射声音的时间比B地晚 秒,A地测得该仪器在A、B、C三地位于同一水平面上,至最高点H时的仰角为30°,求该仪器的垂直弹射高度CH(声音的传播速度为340米/秒)
秒,A地测得该仪器在A、B、C三地位于同一水平面上,至最高点H时的仰角为30°,求该仪器的垂直弹射高度CH(声音的传播速度为340米/秒)