题目内容
由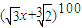 展开所得的x的多项式中,系数为有理数的共有( )
展开所得的x的多项式中,系数为有理数的共有( )A.50项
B.17项
C.16项
D.15项
【答案】分析:根据题意,可得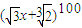 的二项展开式,若x的系数为有理数,即(
的二项展开式,若x的系数为有理数,即(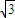 )100-r•(
)100-r•(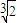 )r为有理数,则100-r为2的倍数,r为3的倍数,设r=3n,则100-3n为2的整数倍,分析可得答案.
)r为有理数,则100-r为2的倍数,r为3的倍数,设r=3n,则100-3n为2的整数倍,分析可得答案.
解答:解:根据题意,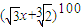 的二项展开式为Tr+1=C100r•(
的二项展开式为Tr+1=C100r•(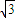 x)100-r•(
x)100-r•(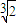 )r=C100r•(
)r=C100r•(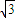 )100-r•(
)100-r•(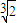 )r•x100-r,
)r•x100-r,
若x的系数为有理数,即(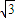 )100-r•(
)100-r•(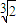 )r为有理数,
)r为有理数,
则100-r为2的倍数,r为3的倍数,
设r=3n,则100-3n为2的整数倍,
分析可得,有17个符合条件,
故选B.
点评:本题考查二项式定理的应用,注意整数的整除的有关性质,仔细进行分析.
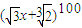 的二项展开式,若x的系数为有理数,即(
的二项展开式,若x的系数为有理数,即(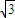 )100-r•(
)100-r•(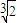 )r为有理数,则100-r为2的倍数,r为3的倍数,设r=3n,则100-3n为2的整数倍,分析可得答案.
)r为有理数,则100-r为2的倍数,r为3的倍数,设r=3n,则100-3n为2的整数倍,分析可得答案.解答:解:根据题意,
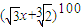 的二项展开式为Tr+1=C100r•(
的二项展开式为Tr+1=C100r•(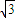 x)100-r•(
x)100-r•(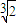 )r=C100r•(
)r=C100r•(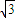 )100-r•(
)100-r•(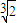 )r•x100-r,
)r•x100-r,若x的系数为有理数,即(
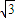 )100-r•(
)100-r•(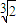 )r为有理数,
)r为有理数,则100-r为2的倍数,r为3的倍数,
设r=3n,则100-3n为2的整数倍,
分析可得,有17个符合条件,
故选B.
点评:本题考查二项式定理的应用,注意整数的整除的有关性质,仔细进行分析.

练习册系列答案
 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
由(
x+
)100展开所得的x的多项式中,系数为有理数的共有( )
| 3 |
| 3 | 2 |
| A、50项 | B、17项 |
| C、16项 | D、15项 |
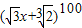 展开所得的x的多项式中,系数为有理数的共有( )
展开所得的x的多项式中,系数为有理数的共有( )