题目内容
 在可行域内任取一点,规则如程序框图所示,求能输出数对(x,y)的概率.
在可行域内任取一点,规则如程序框图所示,求能输出数对(x,y)的概率.分析:本题是一个几何概率模型的问题,由所给的不等式组可以得出,其图形是一个正方形,而所研究的事件对应的图形是一个圆面,求出两个图形的面积即可得到输出的数对的概率.
解答: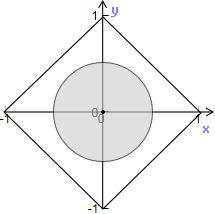 解:满足条件
解:满足条件
的几何图形如下图中矩形所示
满足条件x2+y2≤
的几何图形如下图中阴影所示
其中矩形面积为:S矩形=
×
=2
阴影部分的面积为:S阴影=π(
)2=
则能输出数对(x,y)的概率P=
=
.
 解:满足条件
解:满足条件
|
满足条件x2+y2≤
| 1 |
| 2 |
其中矩形面积为:S矩形=
| 2 |
| 2 |
阴影部分的面积为:S阴影=π(
| ||
| 2 |
| π |
| 2 |
则能输出数对(x,y)的概率P=
| S阴影 |
| S矩形 |
| π |
| 4 |
点评:本题以几何概率模型为背景考查框图之选择结构,题型新颖,解题的关键是通过框图研究出总的基本事件对应的区域面积以及所研究的对象对应的区域的面积来.本题有一定的综合性与抽象性.

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案
相关题目
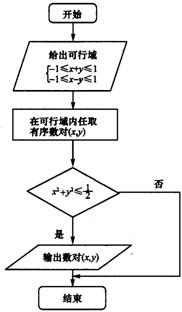 在可行域内任取一点(x,y),如果执行如图的程序框图,那么输出数对(x,y)的概率是( )
在可行域内任取一点(x,y),如果执行如图的程序框图,那么输出数对(x,y)的概率是( )A、
| ||
B、
| ||
C、
| ||
D、
|
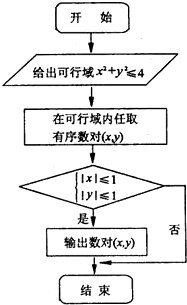 在可行域内任取一点,规则如流程图所示,则能输出数对(x,y)的概率是
在可行域内任取一点,规则如流程图所示,则能输出数对(x,y)的概率是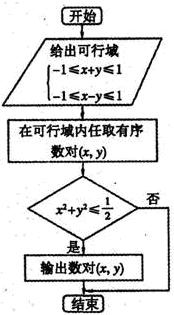 在可行域内任取一点(x,y),如果执行如图的程序框图,那么输出数对(x,y)的概率是
在可行域内任取一点(x,y),如果执行如图的程序框图,那么输出数对(x,y)的概率是 (2012•许昌三模)在可行域内任取一点(x,y),如果执行如图的程序框图,那么输出数对(x,y)的概率是( )
(2012•许昌三模)在可行域内任取一点(x,y),如果执行如图的程序框图,那么输出数对(x,y)的概率是( )