题目内容
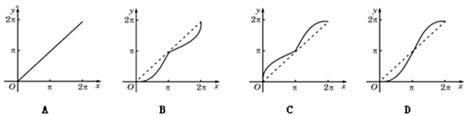
如图,函数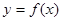 的图象是中心在原点,焦点在
的图象是中心在原点,焦点在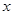 轴上的椭圆的两段弧,则不等式
轴上的椭圆的两段弧,则不等式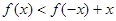 的解集为 ( )
的解集为 ( )

A.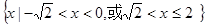
B.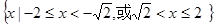
C.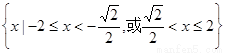
D.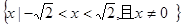
【答案】
A
【解析】
试题分析:由图像知f(x)为奇函数,所以f(-x)=-f(x).所以原不等式可化为f(x)<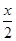 ,
,
由图像易知,包含这两段弧的椭圆方程为 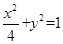 ,
,
与直线y=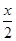 联立得
联立得 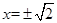 ,
,
结合图像知:不等式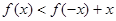 的解集为
的解集为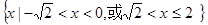 。
。
考点:函数的奇偶性;
点评:本题主要考查奇函数的性质和椭圆的标准方程,体现了数形结合及转化的数学思想.根据已知条件对不等式进行转化变形是解答本题的关键.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案
相关题目
蔬菜基地种植某种蔬菜,由市场行情分析知,1月份至6月份这种蔬菜的上市时间x(月份)与市场售价p(元/千克)的关系如下表:
| 上市时间x(月份) | 1 | 2 | 3 | 4 | 5 | 6 |
| 市场售价p(元/千克) | 10.5 | 9 | 7.5 | 6 | 4.5 | 3 |
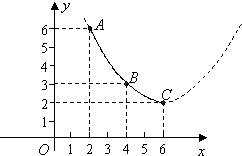
(1)写出上表中表示的市场售价p(元/千克)关于上市时间x(月份)的函数关系式;
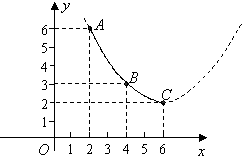
(2)若图中抛物线过A,B,C点,写出抛物线对应的函数关系式;
(3)由以上信息分析,哪个月上市出售这种蔬菜每千克的收益最大?最大值为多少?(收益=市场售价-种植成本)
蔬菜基地种植某种蔬菜,由市场行情分析知,1月份至6月份这种蔬菜的上市时间x(月份)与市场售价p(元/千克)的关系如下表:
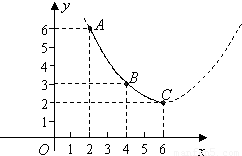
这种蔬菜每千克的种植成本y(元/千克)与上市时间x(月份)满足一个函数关系,这个函数的图象是抛物线的一段(如图).
(1)写出上表中表示的市场售价p(元/千克)关于上市时间x(月份)的函数关系式;
(2)若图中抛物线过A,B,C点,写出抛物线对应的函数关系式;
(3)由以上信息分析,哪个月上市出售这种蔬菜每千克的收益最大?最大值为多少?(收益=市场售价-种植成本)
| 上市时间x(月份) | 1 | 2 | 3 | 4 | 5 | 6 |
| 市场售价p(元/千克) | 10.5 | 9 | 7.5 | 6 | 4.5 | 3 |
(1)写出上表中表示的市场售价p(元/千克)关于上市时间x(月份)的函数关系式;
(2)若图中抛物线过A,B,C点,写出抛物线对应的函数关系式;
(3)由以上信息分析,哪个月上市出售这种蔬菜每千克的收益最大?最大值为多少?(收益=市场售价-种植成本)

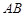 的长为
的长为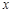 ,
, 表示弧
表示弧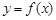 的图象是(
)
的图象是(
)