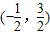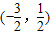题目内容
在实数集上定义运算?:x?y=x(1-y),若不等式(x-a)?(x+a)<1对任意实数x都成立,则实数a的取值范围是( )
| A.(-1,1) | B.(0,2) | C.(-
| D.(-
|
由题知(x-a)?(x+a)=(x-a)[1-(x+a)]=-x2+x+a2-a=-(x-
)2+a2-a+
.
∴不等式(x-a)?(x+a)<1对任意实数x都成立转化为-(x-
)2+a2-a+
<1对任意实数x都成立,
即 a2-a+
<1恒成立,
解可得-
<a<
.
故选C
| 1 |
| 2 |
| 1 |
| 4 |
∴不等式(x-a)?(x+a)<1对任意实数x都成立转化为-(x-
| 1 |
| 2 |
| 1 |
| 4 |
即 a2-a+
| 1 |
| 4 |
解可得-
| 1 |
| 2 |
| 3 |
| 2 |
故选C

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
在实数集上定义运算?:x?y=x(1-y),若不等式(x-a)?(x+a)<1对任意实数x都成立,则实数a的取值范围是( )
| A、(-1,1) | ||||
| B、(0,2) | ||||
C、(-
| ||||
D、(-
|
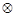 :
: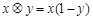 ,若不等式
,若不等式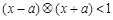 对任意实数
对任意实数 都成立,则实数
都成立,则实数 的取值范围是
的取值范围是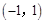 B.
B.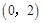 C.
C.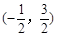 D.
D.