题目内容
为考察某种药物预防疾病的效果,进行动物试验,调查了105个样本,统计结果为:服药的共有55个样本,服药但患病的仍有10个样本,没有服药且未患病的有30个样本.(1)根据所给样本数据完成2×2列联表中的数据;
(2)请问能有多大把握认为药物有效?
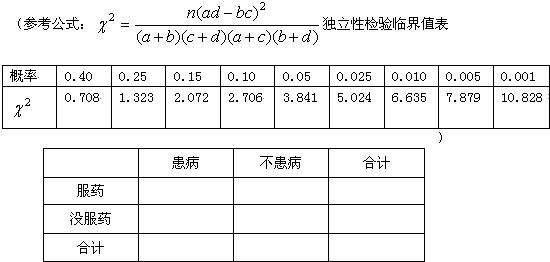
分析:(1)根据服用药的共105个样本,服用药但患病的仍有10个样本,没有服用药且未患病的有30个样本,没有服药且没有患病的有20个,根据各种情况的数据,列出表格,填好数据,得到列联表
(2)根据上一问做出的列联表,看出各种情况的数据,代入求临界值的公式,做出观测值,拿观测值同临界值表进行比较,得到有97.5%的把握认为药物有效.
(2)根据上一问做出的列联表,看出各种情况的数据,代入求临界值的公式,做出观测值,拿观测值同临界值表进行比较,得到有97.5%的把握认为药物有效.
解答:解:(1)解依据题意得,服药但没有病的45人,没有服药且患病的20可列下列22联表
(2)假设服药和患病没有关系,则Χ2的观测值应该很小,
而Χ2=
=6.109.
6.109>5.024,由独立性检验临界值表可以得出,有97.5%的把握药物有效.
| 患病 | 不患病 | 合计 | |
| 服药 | 10 | 45 | 55 |
| 没服药 | 20 | 30 | 50 |
| 合计 | 30 | 75 | 105 |
而Χ2=
| n(ad-bc)2 |
| (a+d)(c+d)(a+c)(b+d) |
6.109>5.024,由独立性检验临界值表可以得出,有97.5%的把握药物有效.
点评:本题考查列联表,独立性检验的应用,是这一部分知识点一个典型的问题,本题解题的关键是注意解题时数字运算要认真,不要出错

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目

