题目内容
(本题10分)已知椭圆与双曲线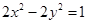 共焦点,且过(
共焦点,且过(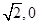 )
)
(1)求椭圆的标准方程;
(2)求斜率为2的一组平行弦的中点轨迹方程。
【答案】
(1)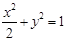
(2)y=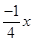 (
(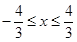
【解析】解:(1)依题意得,将椭圆方程标准化为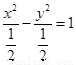 ,则c=1
,则c=1
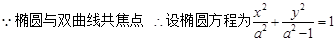
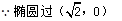
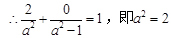

(2)依题意,设斜率为2的弦所在直线的方程为y=2x+b,弦的中点坐标为(x,y),则
 y=2x+b
y=2x+b
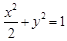 得9x2+8xb+2b2—2=0
得9x2+8xb+2b2—2=0
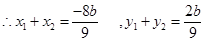
即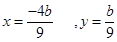 两式消掉b得y=
两式消掉b得y=
令△=0,64b2-36(2b2-2)=0,即b=±3,所以斜率为2,且与椭圆相切的直线方程为y=2x±3
即当x= 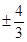 时斜率为2的直线与椭圆相切.
时斜率为2的直线与椭圆相切.
所以平行弦得中点轨迹方程为:y=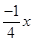 (
(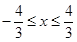 )
)

练习册系列答案
相关题目
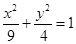 与坐标轴正半轴的两交点,在第一象限的椭圆弧上求一点P,使四边形OPAB的面积最大.
与坐标轴正半轴的两交点,在第一象限的椭圆弧上求一点P,使四边形OPAB的面积最大.