题目内容
已知f(x)=lnx(x>0),f(x)的导数是f′(x),若a=f(7),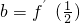 ,
,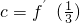 ,则a、b、c的大小关系是
,则a、b、c的大小关系是
- A.c<b<a
- B.a<b<c
- C.b<c<a
- D.b<a<c
B
分析:利用导数的运算法则求出f′(x)= ,得到a=f(7)=ln7,
,得到a=f(7)=ln7,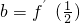 =2,
=2,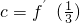 =3,利用对数函数的单调性判断出ln7<lne2=2,得到选项.
=3,利用对数函数的单调性判断出ln7<lne2=2,得到选项.
解答:f′(x)= ,
,
a=f(7)=ln7,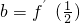 =2,
=2,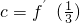 =3,
=3,
因为ln7<lne2=2,
所以a<b<c
故选B.
点评:本题考查导函数的运算法则及利用函数的单调性比较函数值的大小,属于基础题.
分析:利用导数的运算法则求出f′(x)=
 ,得到a=f(7)=ln7,
,得到a=f(7)=ln7,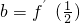 =2,
=2,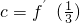 =3,利用对数函数的单调性判断出ln7<lne2=2,得到选项.
=3,利用对数函数的单调性判断出ln7<lne2=2,得到选项.解答:f′(x)=
 ,
,a=f(7)=ln7,
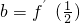 =2,
=2,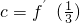 =3,
=3,因为ln7<lne2=2,
所以a<b<c
故选B.
点评:本题考查导函数的运算法则及利用函数的单调性比较函数值的大小,属于基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目