题目内容
阅读与理解:
给出公式:sin(α+β)=sinαcosβ+cosαsinβ;cos(α-β)=cosαcosβ+sinαsinβ;我们可以根据公式将函数g(x)=sinx+
cosx化为:g(x)=2(
sinx+
cosx)=2(sinxcos
+cosxsin
)=2sin(x+
)
(1)根据你的理解将函数f(x)=sinx+cos(x-
)化为f(x)=Asin(ωx+φ)的形式.
(2)求出上题函数f(x)的最小正周期、对称中心及单调递增区间.
给出公式:sin(α+β)=sinαcosβ+cosαsinβ;cos(α-β)=cosαcosβ+sinαsinβ;我们可以根据公式将函数g(x)=sinx+
| 3 |
| 1 |
| 2 |
| ||
| 2 |
| π |
| 3 |
| π |
| 3 |
| π |
| 3 |
(1)根据你的理解将函数f(x)=sinx+cos(x-
| π |
| 6 |
(2)求出上题函数f(x)的最小正周期、对称中心及单调递增区间.
分析:(1)利用三角函数的恒等变换化简函数f(x)的解析式为
sin(x+
).
(2)由(1)可得函数的最小正周期 T=2π.令x+
=kπ,k∈z,求得 x=kπ-
,可得函数的中心.令 2kπ-
≤x+
≤2kπ+
,k∈z,求得x的范围,可得递增区间.
| 3 |
| π |
| 6 |
(2)由(1)可得函数的最小正周期 T=2π.令x+
| π |
| 6 |
| π |
| 6 |
| π |
| 2 |
| π |
| 6 |
| π |
| 2 |
解答:解:(1)函数f(x)=sinx+cos(x-
)=sinx+
cosx+
sinx=
sinx+
cosx
=
(
sinx+
cosx)=
sin(x+
).
(2)由(1)可得函数的最小正周期 T=2π,
令x+
=kπ,k∈z,求得 x=kπ-
,
故函数的中心为 (kπ-
,0),k∈z.
令 2kπ-
≤x+
≤2kπ+
,k∈z,求得 2kπ-
≤x≤2kπ+
,
故递增区间为[2kπ-
,2kπ+
],k∈z.
| π |
| 6 |
| ||
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
| ||
| 2 |
=
| 3 |
| ||
| 2 |
| 1 |
| 2 |
| 3 |
| π |
| 6 |
(2)由(1)可得函数的最小正周期 T=2π,
令x+
| π |
| 6 |
| π |
| 6 |
故函数的中心为 (kπ-
| π |
| 6 |
令 2kπ-
| π |
| 2 |
| π |
| 6 |
| π |
| 2 |
| 2π |
| 3 |
| π |
| 3 |
故递增区间为[2kπ-
| 2π |
| 3 |
| π |
| 3 |
点评:本题主要考查三角函数的恒等变换及化简求值,三角函数的周期性、单调性、对称性和求法,属于中档题.

练习册系列答案
相关题目
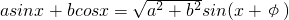 给出公式:
给出公式: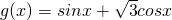 化为:
化为: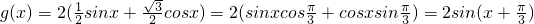
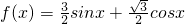 化为f(x)=Asin(ωx+φ)的形式.
化为f(x)=Asin(ωx+φ)的形式.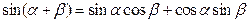 ;
; ;
;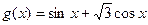 化为:
化为: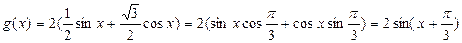
 化为
化为 的形式.
的形式. 的最小正周期、对称中心.
的最小正周期、对称中心.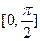 上的最大值、最小值及相应的
上的最大值、最小值及相应的 的值。
的值。 cosx化为:g(x)=2(
cosx化为:g(x)=2( sinx+
sinx+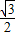 cosx)=2(sinxcos
cosx)=2(sinxcos +cosxsin
+cosxsin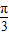 )=2sin(x+
)=2sin(x+ )
) )化为f(x)=Asin(ωx+φ)的形式.
)化为f(x)=Asin(ωx+φ)的形式.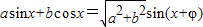 给出公式:
给出公式: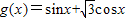 化为:
化为: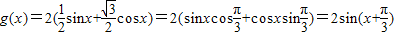
 化为f(x)=Asin(ωx+φ)的形式.
化为f(x)=Asin(ωx+φ)的形式.