题目内容
已知等差数列{an}的首项为p,公差为d(d>0).对于不同的自然数n,直线x=an与x轴和指数函数 的图象分别交于点An与Bn(如图所示),记Bn的坐标为(an,bn),直角梯形A1A2B2B1、A2A3B3B2的面积分别为s1和s2,一般地记直角梯形AnAn+1Bn+1Bn的面积为sn.
的图象分别交于点An与Bn(如图所示),记Bn的坐标为(an,bn),直角梯形A1A2B2B1、A2A3B3B2的面积分别为s1和s2,一般地记直角梯形AnAn+1Bn+1Bn的面积为sn.(1)求证数列{sn}是公比绝对值小于1的等比数列;
(2)设{an}的公差d=1,是否存在这样的正整数n,构成以bn,bn+1,bn+2为边长的三角形?并请说明理由;
(3)(理科做,文科不做)设{an}的公差d=1,是否存在这样的实数p使得(1)中无穷等比数列{sn}各项的和S>2010?如果存在,给出一个符合条件的p值;如果不存在,请说明理由.(参考数据:210=1024)

【答案】分析:(1)an=p+(n-1)d,直角梯形AnAn+1Bn+1Bn的两底长度AnBn=f(an),An+1Bn+1=f(an+1).高为AnAn+1 =d,利用梯形面积公式表示出sn.利用等比数列定义进行证明即可.
(2)an=-1+(n-1)=n-2,bn=( )n-2,以bn,bn+1,bn+2为边长能构成一个三角形,则bn+2+bn+1>bn考查次不等式解的情况作解答.
)n-2,以bn,bn+1,bn+2为边长能构成一个三角形,则bn+2+bn+1>bn考查次不等式解的情况作解答.
(4)利用无穷等比数列求和公式,将S>2010 化简为 S=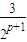 >2010,探讨p的存在性.
>2010,探讨p的存在性.
解答:解:(1)由等差数列通项公式可得an=p+(n-1)d,
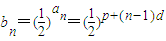 …(2分)
…(2分)
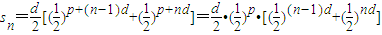 ,
,
对于任意自然数n,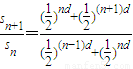 =
=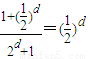 ,
,
所以数列{sn}是等比数列且公比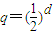 ,因为d>0,所以|q|<1.…(5分)
,因为d>0,所以|q|<1.…(5分)
(写成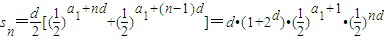 ,得公比
,得公比 也可)
也可)
(2)an=p+(n-1)=n+p-1,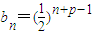 ,对每个正整数n,bn>bn+1>bn+2
,对每个正整数n,bn>bn+1>bn+2
若以bn,bn+1,bn+2为边长能构成一个三角形,则bn+2+bn+1>bn,
即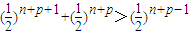 ,令n=-1,得1+2>4,这是不可能的.
,令n=-1,得1+2>4,这是不可能的.
所以对每一个正整数n,以bn,bn+1,bn+2为边长不能构成三角形.…(10分)
(3)(理科做,文科不做)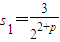 ,
,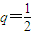 所以
所以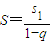 =
=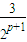
如果存在p使得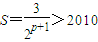 ,即
,即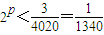
两边取对数得:p<-log21340,
因此符合条件的p值存在,log21340≈10.4,可取p=-11等.…(14分)
说明:通过具体的p值,验证 也可.
也可.
点评:本题是函数与数列、不等式的结合.考查等比数列的判定,含参数不等式解的讨论.考查分析解决问题,计算,逻辑思维等能力
(2)an=-1+(n-1)=n-2,bn=(
 )n-2,以bn,bn+1,bn+2为边长能构成一个三角形,则bn+2+bn+1>bn考查次不等式解的情况作解答.
)n-2,以bn,bn+1,bn+2为边长能构成一个三角形,则bn+2+bn+1>bn考查次不等式解的情况作解答.(4)利用无穷等比数列求和公式,将S>2010 化简为 S=
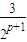 >2010,探讨p的存在性.
>2010,探讨p的存在性.解答:解:(1)由等差数列通项公式可得an=p+(n-1)d,
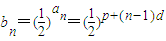 …(2分)
…(2分)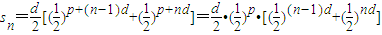 ,
,对于任意自然数n,
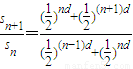 =
=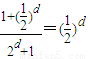 ,
,所以数列{sn}是等比数列且公比
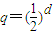 ,因为d>0,所以|q|<1.…(5分)
,因为d>0,所以|q|<1.…(5分)(写成
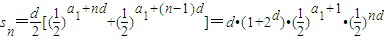 ,得公比
,得公比 也可)
也可)(2)an=p+(n-1)=n+p-1,
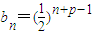 ,对每个正整数n,bn>bn+1>bn+2
,对每个正整数n,bn>bn+1>bn+2若以bn,bn+1,bn+2为边长能构成一个三角形,则bn+2+bn+1>bn,
即
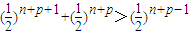 ,令n=-1,得1+2>4,这是不可能的.
,令n=-1,得1+2>4,这是不可能的.所以对每一个正整数n,以bn,bn+1,bn+2为边长不能构成三角形.…(10分)
(3)(理科做,文科不做)
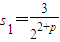 ,
,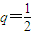 所以
所以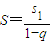 =
=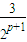
如果存在p使得
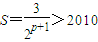 ,即
,即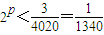
两边取对数得:p<-log21340,
因此符合条件的p值存在,log21340≈10.4,可取p=-11等.…(14分)
说明:通过具体的p值,验证
 也可.
也可.点评:本题是函数与数列、不等式的结合.考查等比数列的判定,含参数不等式解的讨论.考查分析解决问题,计算,逻辑思维等能力

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 已知等差数列{an}中,a4a6=-4,a2+a8=0,n∈N*.
已知等差数列{an}中,a4a6=-4,a2+a8=0,n∈N*.