题目内容
(1)证明:sin4θ+sin2θcos2θ+cos2θ=1
(2)计算:sin
π+cos
π+tan(-
π).
(2)计算:sin
| 25 |
| 6 |
| 25 |
| 3 |
| 25 |
| 4 |
(1)证明:左边=sin4θ+sin2θcos2θ+cos2θ=sin2θ(sin2θ+cos2θ)+cos2θ=sin2θ+cos2θ=1=右边,
则原式成立;
(2)原式=sin(4π+
)+cos(8π+
)-tan(6π+
)=sin
+cos
-tan
=
+
-1=1-1=0.
则原式成立;
(2)原式=sin(4π+
| π |
| 6 |
| π |
| 3 |
| π |
| 4 |
| π |
| 6 |
| π |
| 3 |
| π |
| 4 |
| 1 |
| 2 |
| 1 |
| 2 |

练习册系列答案
相关题目
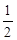 ,再将图像沿
,再将图像沿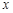 轴向右平移
轴向右平移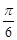 个单位,得到函数
个单位,得到函数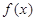 的图像.
的图像.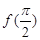 .
.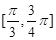 上的值域.
上的值域.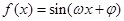 (
(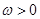 ,
, )为偶函数,其图象上相邻的两个对称轴之间的距离为
)为偶函数,其图象上相邻的两个对称轴之间的距离为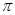 .
.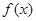 的解析式;
的解析式;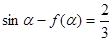 ,求
,求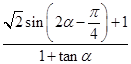 的值.
的值. ,则
,则 ( )
( )
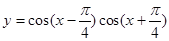 的图象中相邻两个对称中心的距离为
的图象中相邻两个对称中心的距离为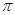 ,②
,②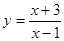 的图象关于点
的图象关于点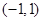 对称,③关于
对称,③关于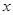 的方程
的方程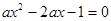 有且仅有一个实根,则
有且仅有一个实根,则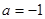 ,④命题
,④命题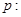 对任意
对任意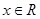 ,都有
,都有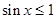 ;则
;则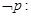 存在
存在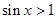 .其中真命题的序号是_________________________ .
.其中真命题的序号是_________________________ .


