题目内容
已知一元二次函数y=f(x)满足f(-1)=12,且不等式f(x)<0的解集是{x|0<x<5},当a<0时,解关于x的不等式 .
.
【答案】分析:设出二次函数,通过满足f(-1)=12,且不等式f(x)<0的解集是{x|0<x<5},求出函数的表达式,化简表达式为同解不等式,对a分类讨论求出不等式的解集即可.
解答:解:依题意设f(x)=b(x-0)(x-5)=bx(x-5),且b>0,
又f(-1)=12⇒b=2,∴f(x)=2x2-10x,
∴原不等式
化为 ,?(ax+5)x(2x-10)>0
,?(ax+5)x(2x-10)>0
 ?
? ,
,
令 得x1=0,
得x1=0, ,x3=5
,x3=5
当a=-1时,不等式的解为x<0;
当-1<a<0时,5<- ,
,
不等式的解为x<0或5<x<- ;
;
当a<-1时,5>- >0,
>0,
不等式的解:x<0或5>x>- ;
;
综上所述:当-1<a<0时,
不等式的解集为{x|x<0或5<x<- };
};
当a=-1时,不等式的解为{x|x<0};
当a<-1时,不等式的解:{x|x<0或5>x>- };(12分)
};(12分)
点评:本题考查不等式的解法,注意分类讨论穿根法的应用,二次函数的求法,考查计算能力.
解答:解:依题意设f(x)=b(x-0)(x-5)=bx(x-5),且b>0,
又f(-1)=12⇒b=2,∴f(x)=2x2-10x,
∴原不等式

化为
 ,?(ax+5)x(2x-10)>0
,?(ax+5)x(2x-10)>0 ?
? ,
,令
 得x1=0,
得x1=0, ,x3=5
,x3=5当a=-1时,不等式的解为x<0;
当-1<a<0时,5<-
 ,
,不等式的解为x<0或5<x<-
 ;
;当a<-1时,5>-
 >0,
>0,不等式的解:x<0或5>x>-
 ;
;综上所述:当-1<a<0时,
不等式的解集为{x|x<0或5<x<-
 };
};当a=-1时,不等式的解为{x|x<0};
当a<-1时,不等式的解:{x|x<0或5>x>-
 };(12分)
};(12分)点评:本题考查不等式的解法,注意分类讨论穿根法的应用,二次函数的求法,考查计算能力.

练习册系列答案
相关题目
 ,求该一元二次函数的解析式。
,求该一元二次函数的解析式。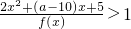 .
.