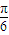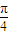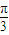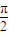题目内容
己知双曲线的方程为x2-
=1,直线m的方程为x=
,过双曲线的右焦点F的直线l与双曲线的右支相交于P、Q,以PQ为直径的圆与直线m相交于M、N,记劣弧
的长度为n,则
的值为( )
| y2 |
| 3 |
| 1 |
| 2 |
 |
| MN |
| n |
| |PQ| |
A、
| ||
B、
| ||
C、
| ||
D、
|
分析:由直角梯形的中位线性质可得:d=
,再利用双曲线的第二定义可得r=d1+d2,即可得到∠MEN=
,即可根据弧长公式得到弧长,进而得到答案.
| d1+d2 |
| 2 |
| 2π |
| 3 |
解答:解:设P、Q到右准线的距离分别等于 d1、d2,AB的中点为E,E到右准线的距离等于d,并且圆的半径等于r=
,
由直角梯形的中位线性质可得:d=
,
再根据双曲线的第二定义可得:
=e=2,
=e=2,
所以|PF|+|QF|=2(d1+d2)=2r,
所以r=d1+d2,
即可得到r=2d,
所以∠MEN=
,则有
的长度为n=
,
所以
=
=
.
故选C.
| |PQ| |
| 2 |
由直角梯形的中位线性质可得:d=
| d1+d2 |
| 2 |
再根据双曲线的第二定义可得:
| |PF| |
| d1 |
| |QF| |
| d2 |
所以|PF|+|QF|=2(d1+d2)=2r,
所以r=d1+d2,
即可得到r=2d,
所以∠MEN=
| 2π |
| 3 |
 |
| MN |
| 2πr |
| 3 |
所以
| n |
| |PQ| |
| ||
| 2r |
| π |
| 3 |
故选C.
点评:本题考查双曲线的第二定义和标准方程,以及双曲线的简单性质的应用与圆的有关性质及其应用.

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目
 =1,直线m的方程为x=
=1,直线m的方程为x= ,过双曲线的右焦点F的直线l与双曲线的右支相交于P、Q,以PQ为直径的圆与直线m相交于M、N,记劣弧
,过双曲线的右焦点F的直线l与双曲线的右支相交于P、Q,以PQ为直径的圆与直线m相交于M、N,记劣弧 的长度为n,则
的长度为n,则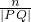 的值为
的值为



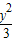 =1,直线m的方程为x=
=1,直线m的方程为x= ,过双曲线的右焦点F的直线l与双曲线的右支相交于P、Q,以PQ为直径的圆与直线m相交于M、N,记劣弧
,过双曲线的右焦点F的直线l与双曲线的右支相交于P、Q,以PQ为直径的圆与直线m相交于M、N,记劣弧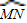 的长度为n,则
的长度为n,则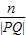 的值为( )
的值为( )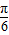
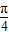
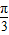
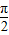
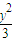 =1,直线m的方程为x=
=1,直线m的方程为x= ,过双曲线的右焦点F的直线l与双曲线的右支相交于P、Q,以PQ为直径的圆与直线m相交于M、N,记劣弧
,过双曲线的右焦点F的直线l与双曲线的右支相交于P、Q,以PQ为直径的圆与直线m相交于M、N,记劣弧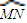 的长度为n,则
的长度为n,则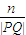 的值为( )
的值为( )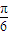
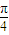

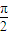
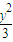 =1,直线m的方程为x=
=1,直线m的方程为x= ,过双曲线的右焦点F的直线l与双曲线的右支相交于P、Q,以PQ为直径的圆与直线m相交于M、N,记劣弧
,过双曲线的右焦点F的直线l与双曲线的右支相交于P、Q,以PQ为直径的圆与直线m相交于M、N,记劣弧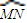 的长度为n,则
的长度为n,则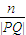 的值为( )
的值为( )