题目内容
(坐标系与参数方程选做题)已知抛物线C的参数方程为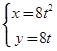 (t为参数),若斜率为1的直线经过抛物线C的焦点,且与圆
(t为参数),若斜率为1的直线经过抛物线C的焦点,且与圆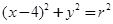 (r>0)相切,则r=
(r>0)相切,则r=
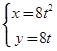 (t为参数),若斜率为1的直线经过抛物线C的焦点,且与圆
(t为参数),若斜率为1的直线经过抛物线C的焦点,且与圆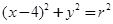 (r>0)相切,则r=
(r>0)相切,则r= 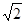
解:∵抛物线C的参数方程为
x=8t2
y=8t
则抛物线的标准方程为:y2=8x
则抛物线C的焦点的坐标为(2,0)
又∵斜率为1的直线经过抛物线C的焦点
则直线的方程为y=x-2,即经x-y-2=0
由直线与圆(x-4)2+y2=r2,则
r=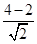 =
=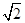
故答案为: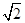
x=8t2
y=8t
则抛物线的标准方程为:y2=8x
则抛物线C的焦点的坐标为(2,0)
又∵斜率为1的直线经过抛物线C的焦点
则直线的方程为y=x-2,即经x-y-2=0
由直线与圆(x-4)2+y2=r2,则
r=
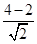 =
=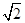
故答案为:

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
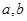 是方程x
是方程x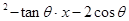 =0的两个实根,那么过点
=0的两个实根,那么过点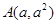 和
和 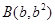 (
( )的直线与曲线
)的直线与曲线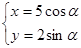 (
(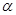 为参数)的位置关系是
为参数)的位置关系是 在直角坐标系
在直角坐标系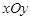 中, 过点
中, 过点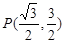 作倾斜角为
作倾斜角为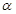 的直线
的直线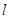 与曲线
与曲线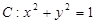 相交于不同的两点
相交于不同的两点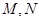 .
.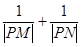 的取值范围.
的取值范围.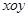 中,曲线C1的参数方程为
中,曲线C1的参数方程为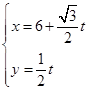 (t为参数);在以O为极点,x轴的正半轴为极轴的极坐标系中,曲线C2的极坐标方程为
(t为参数);在以O为极点,x轴的正半轴为极轴的极坐标系中,曲线C2的极坐标方程为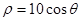 ,曲线C1与C2交于A、B两点,求|AB|.
,曲线C1与C2交于A、B两点,求|AB|.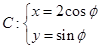 (
(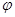 为参数),若点
为参数),若点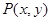 是曲线
是曲线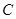 上的动点
上的动点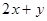 的取值范围
的取值范围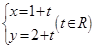 被曲线C截得的弦长
被曲线C截得的弦长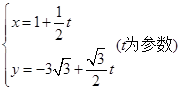 和圆
和圆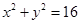 交于
交于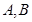 两点,
两点,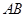 的中点坐标为
的中点坐标为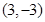
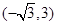
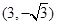
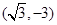
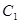 的参数方程为
的参数方程为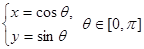 ,以原点为极点,以
,以原点为极点,以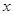 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线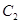 在极坐标系中的方程为
在极坐标系中的方程为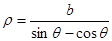 .若曲线
.若曲线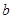 的取值范围是 。
的取值范围是 。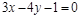 被曲线
被曲线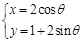 (
(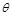 为参数)所截得的弦长为_________.
为参数)所截得的弦长为_________.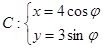 (
(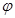 为参数).
为参数).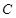 的方程化为普通方程;
的方程化为普通方程;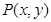 是曲线
是曲线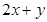 的取值范围.
的取值范围.