题目内容
设Sn是首项为4,公差d≠0的等差数列{an}的前n项和,若| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 5 |
(1){an}的通项公式an;
(2)使Sn>0的最大n值.
分析:(1)由题设知首项为4,且
S3和
S4的等比中项为
S5由此建立方程即可求出公差d,从而求出其通项公式;
(2)由(1)的结论,利用数列的通项公式求出前n和的最大值是S2,根据等差数列前n项和公式的函数特性即可得出使Sn>0的最大n值.
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 5 |
(2)由(1)的结论,利用数列的通项公式求出前n和的最大值是S2,根据等差数列前n项和公式的函数特性即可得出使Sn>0的最大n值.
解答:解:(1)由条件得:
=
,(4分)
∵Sn=a1n+
n(n-1)d,
∴(12+5d)d=0,∵d≠0,得d=-
,
∴an=
.(5分)
(2)由an=
>0,
得n<
,∴n=2时,Sn取最大值,
∴使Sn>0的最大n的值为4.(5分)
| S3S4 |
| 12 |
| ||
| 25 |
∵Sn=a1n+
| 1 |
| 2 |
∴(12+5d)d=0,∵d≠0,得d=-
| 12 |
| 5 |
∴an=
| -12n+32 |
| 5 |
(2)由an=
| -12n+32 |
| 5 |
得n<
| 8 |
| 3 |
∴使Sn>0的最大n的值为4.(5分)
点评:本题考查等数列与等比数列的综合,考查由题设条件建立方程求公差,及根据通项公式求出数列的通项,由通项的求出数列前n项和的最大值以及由其函数特性判断出使Sn>0的最大n值,求解本题的关键是掌握了等差数列前n项和的函数特性-对称性.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 S3和
S3和 S4的等比中项为
S4的等比中项为 S5.求:
S5.求: S3和
S3和 S4的等比中项为
S4的等比中项为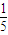 S5.求:
S5.求: