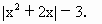题目内容
分别画出下列函数的图象，并写出下列函数的值域：
（1）y=x2-4x+6，x∈[1，5）；
（2）f(x)=
， x∈[3，5]．
（1）y=x2-4x+6，x∈[1，5）；
（2）f(x)=
| x-1 | x+2 |
分析：（1）先配方，从而可得函数的图象；由图象可得当x=2时，y取得最小值2，x=5时，y有最大值11，从而可得结论；
（2）利用图形变换，作出函数的图形，可知函数在[3，5]上是增函数，从而可得函数的值域．
（2）利用图形变换，作出函数的图形，可知函数在[3，5]上是增函数，从而可得函数的值域．
解答：解：（1）配方得：y=x2-4x+6=（x-2）2+2，函数的图象如图所示．
由图象可得当x=2时，y取得最小值2，x=5时，y=11，从而函数的值域为{y|2≤y＜11}．
（2）f(x)=
=1-
， x∈[3，5]，函数图象如图所示
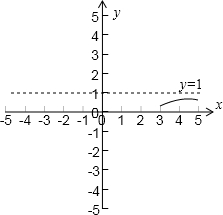
由图象知，函数在[3，5]上是增函数，所以函数的值域为[
，
]．
由图象可得当x=2时，y取得最小值2，x=5时，y=11，从而函数的值域为{y|2≤y＜11}．
（2）f(x)=
| x-1 |
| x+2 |
| 3 |
| x+2 |
由图象知，函数在[3，5]上是增函数，所以函数的值域为[
| 2 |
| 5 |
| 4 |
| 7 |
点评：本题考查函数图象的作法，考查函数的值域，正确作出函数的图象是关键．
练习册系列答案
相关题目
（2006•静安区二模）某种洗衣机在洗涤衣服时，需经过进水、清洗、排水、脱水四个连续的过程．假设进水时水量匀速增加，清洗时水量保持不变．已知进水时间为4分钟，清洗时间为12分钟，排水时间为2分钟，脱水时间为2分钟．洗衣机中的水量y（升）与时间x（分钟）之间的关系如下表所示：
或y＝c(x－20)2＋d(其中a、b、c、d为常数)，作为在排水阶段的2分钟内水量y与时间x之间关系的模拟函数．试分别求出这两个函数的解析式．
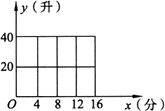
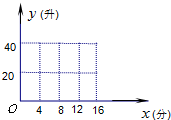某种洗衣机在洗涤衣服时，需经过进水、清洗、排水、脱水四个连续的过程．假设进水时水量匀速增加，清洗时水量保持不变．已知进水时间为4分钟，清洗时间为12分钟，排水时间为2分钟，脱水时间为2分钟．洗衣机中的水量y（升）与时间x（分钟）之间的关系如下表所示：
| x | 0 | 2 | 4 | 16 | 16.5 | 17 | 18 | … |
| y | 0 | 20 | 40 | 40 | 29.5 | 20 | 2 | … |
（1）试写出当x∈[0，16]时y关于x的函数解析式，并画出该函数的图象；
（2）根据排水阶段的2分钟点（x，y）的分布情况，可选用
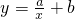或y=c（x-20）2+d（其中a、b、c、d为常数），作为在排水阶段的2分钟内水量y与时间x之间关系的模拟函数．试分别求出这两个函数的解析式；（3）请问（2）中求出的两个函数哪一个更接近实际情况？（写出必要的步骤）