题目内容
在2008年北京奥运会某项目的选拔比赛中,A、B两个代表队进行对抗赛,每队三名队员,A队队员是A1、A2、A3,B队队员是B1、B2、B3,按以往多次比赛的统计,对阵队员之间胜负概率如下表,现按表中对阵方式出场进行三场比赛,每场胜队得1分,负队得0分,设A队、B队最后所得总分分别为ξ、η,且ξ+η=3.| 对阵队员 | A队队员胜 | A队队员负 |
| A1对B1 |  |  |
| A2对B2 | 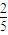 | 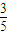 |
| A3对B3 |  |  |
(Ⅱ)求ξ的分布列;并用统计学的知识说明哪个队实力较强.
【答案】分析:(1)A队得分为1分包括第一个队员胜且后两个负,第二个队员胜且一三两个队员负,第三个队员胜且一二两个负,相互独立事件同时发生的概率.
(2)看出随机变量的可能的取值,求出各个取值对应的概率,得到分布列,求出期望,比较两个期望的大小,得到结论.
解答:解:(Ⅰ)设A队得分为(1分)的事件为A,
∴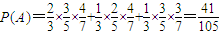 .
.
(Ⅱ)ξ的可能取值为3,2,1,0; ,
,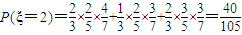
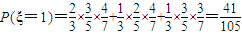 ,
,
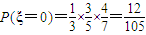 ,
,
∴ξ的分布列为:
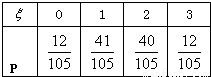
于是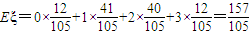 ,
,
∵ξ+η=3,
∴ .
.
由于Eη>Eξ,故B队比A队实力较强.
点评:本题主要考查的是随机变量的分布列和数学期望问题.这是概率与统计大题考查的主阵地,预计还有可能与函数、导数、方程、数列以及不等式等知识综合考查.
(2)看出随机变量的可能的取值,求出各个取值对应的概率,得到分布列,求出期望,比较两个期望的大小,得到结论.
解答:解:(Ⅰ)设A队得分为(1分)的事件为A,
∴
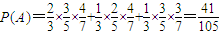 .
.(Ⅱ)ξ的可能取值为3,2,1,0;
 ,
,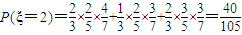
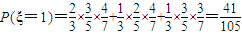 ,
,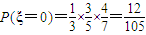 ,
,∴ξ的分布列为:

于是
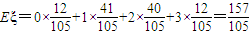 ,
,∵ξ+η=3,
∴
 .
.由于Eη>Eξ,故B队比A队实力较强.
点评:本题主要考查的是随机变量的分布列和数学期望问题.这是概率与统计大题考查的主阵地,预计还有可能与函数、导数、方程、数列以及不等式等知识综合考查.

练习册系列答案
相关题目
 在2008年北京奥运会青岛奥帆赛举行之前,为确保赛事安全,青岛海事部门举行奥运安保海上安全演习.为了测量正在海面匀速行驶的某航船的速度,在海岸上选取距离为1千米的两个观察点C,D,在某天10:00观察到该航船在A处,此时测得∠ADC=30°,3分钟后该船行驶至B处,此时测得∠ACB=60°,∠BCD=45°,∠ADB=60°,则船速为
在2008年北京奥运会青岛奥帆赛举行之前,为确保赛事安全,青岛海事部门举行奥运安保海上安全演习.为了测量正在海面匀速行驶的某航船的速度,在海岸上选取距离为1千米的两个观察点C,D,在某天10:00观察到该航船在A处,此时测得∠ADC=30°,3分钟后该船行驶至B处,此时测得∠ACB=60°,∠BCD=45°,∠ADB=60°,则船速为 在2008年北京奥运会上,林跃.火亮为观众上演了一场精彩的表演,最终以468.18的高分毫无悬念的夺得男子10米比双人跳台的冠军,这次比赛共有7名裁判打分,在第二轮跳水中,林跃.火亮的难度系数为2.0,7名评委给他们评定的成绩分别是:10,9.5,10,10,9.5,10,10,程序框图用来编写程序统计每位选手的成绩,试根据下面所给条件回答下列问题:
在2008年北京奥运会上,林跃.火亮为观众上演了一场精彩的表演,最终以468.18的高分毫无悬念的夺得男子10米比双人跳台的冠军,这次比赛共有7名裁判打分,在第二轮跳水中,林跃.火亮的难度系数为2.0,7名评委给他们评定的成绩分别是:10,9.5,10,10,9.5,10,10,程序框图用来编写程序统计每位选手的成绩,试根据下面所给条件回答下列问题: