题目内容
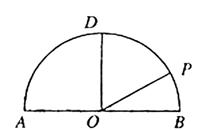
如图,在以点O为圆心,AB为直径的半圆中,D为半圆弧的中点, P为半圆弧上一点,且AB=4,∠POB=30°,双曲线C以A,B为焦点且经过点P.
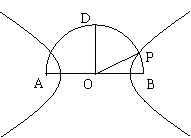 (Ⅰ)建立适当的平面直角坐标系,求双曲线C的方程;
(Ⅰ)建立适当的平面直角坐标系,求双曲线C的方程;
(Ⅱ)设过点D的直线l与双曲线C相交于不同两点E、F,
若△OEF的面积不小于2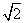 ,求直线l的斜率的取值范围.
,求直线l的斜率的取值范围.
(Ⅰ)方法一:以O为原点,AB、OD所在直线分别
为x轴、y轴建立平面直角坐标系,则
点A(-2,0),B(2,0),P( ,1). (2分)
,1). (2分)
设双曲线实半轴长为a,虚半轴长为b,半焦距为c,则
2a=|PA|-|PB|= ,2c=|AB|=4.
(3分)
,2c=|AB|=4.
(3分)
所以a= ,c=2,从而b2=c2-a2=2.
(4分)
,c=2,从而b2=c2-a2=2.
(4分)
故双曲线C的方程是 .
(5分)
.
(5分)
方法二:以O为原点,AB、OD所在直线分别为x轴、y轴建立平面直角坐标系,则
点A(-2,0),B(2,0),P( ,1).
(2分)
,1).
(2分)
设双曲线C的方程为 >0,b>0),则
>0,b>0),则 .
(3分)
.
(3分)
解得a2=b2=2,故双曲线C的方程是 (5分)
(5分)
(Ⅱ)据题意可设直线l的方程为y=kx+2,代入双曲线C的方程得, ,即
,即
(1-k2)x2-4kx-6=0. (6分)
因为直线l与双曲线C相交于不同两点E、F,则


 即
即  (7分)
(7分)
设点E(x1,y1),F(x2,y2),则x1+x2= .
(8分)
.
(8分)
所以|EF|=
= (9分)
(9分)
又原点O到直线l的距离d= .
(10分)
.
(10分)
所以S△DEF= (11分)因为S△OEF
(11分)因为S△OEF ,则
,则 (12分)
(12分)
综上分析,直线l的斜率的取值范围是[- ,-1)
,-1) (-1,1)
(-1,1) (1,
(1, ]. (13分)
]. (13分)

 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案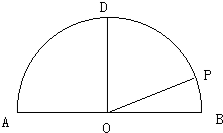 如图,在以点O为圆心,|AB|=4为直径的半圆ADB中,OD⊥AB,P是半圆弧上一点,∠POB=30°,曲线C是满足||MA|-|MB||为定值的动点M的轨迹,且曲线C过点P.
如图,在以点O为圆心,|AB|=4为直径的半圆ADB中,OD⊥AB,P是半圆弧上一点,∠POB=30°,曲线C是满足||MA|-|MB||为定值的动点M的轨迹,且曲线C过点P.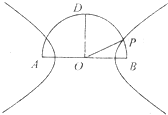 如图,在以点O为圆心,AB为直径的半圆中,D为半圆弧的中心,P为半圆弧上一点,且AB=4,∠POB=30°,双曲线C以A,B为焦点且经过点P.
如图,在以点O为圆心,AB为直径的半圆中,D为半圆弧的中心,P为半圆弧上一点,且AB=4,∠POB=30°,双曲线C以A,B为焦点且经过点P.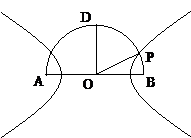
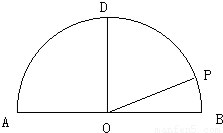 如图,在以点O为圆心,|AB|=4为直径的半圆ADB中,OD⊥AB,P是半圆弧上一点,∠POB=30°,曲线C是满足||MA|-|MB||为定值的动点M的轨迹,且曲线C过点P.
如图,在以点O为圆心,|AB|=4为直径的半圆ADB中,OD⊥AB,P是半圆弧上一点,∠POB=30°,曲线C是满足||MA|-|MB||为定值的动点M的轨迹,且曲线C过点P.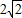 ,求直线l斜率的取值范围.
,求直线l斜率的取值范围.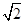 ,求直线l斜率的取值范围。
,求直线l斜率的取值范围。