题目内容
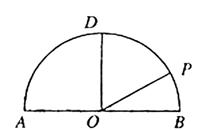
 如图,在以点O为圆心,|AB|=4为直径的半圆ADB中,OD⊥AB,P是半圆弧上一点,∠POB=30°,曲线C是满足||MA|-|MB||为定值的动点M的轨迹,且曲线C过点P.
如图,在以点O为圆心,|AB|=4为直径的半圆ADB中,OD⊥AB,P是半圆弧上一点,∠POB=30°,曲线C是满足||MA|-|MB||为定值的动点M的轨迹,且曲线C过点P.(Ⅰ)建立适当的平面直角坐标系,求曲线C的方程;
(Ⅱ)设过点D的直线l与曲线C相交于不同的两点E、F.若△OEF的面积不小于2
| 2 |
分析:(Ⅰ)以O为原点,AB、OD所在直线分别为x轴、y轴,建立平面直角坐标系,由题意得|MA|-|MB|=|PA|-|PB|=
-
=2
<|AB|=4.由此可知曲线C的方程;
(Ⅱ)依题意,可设直线l的方程为y=kx+2,代入双曲线C的方程并整理,得(1-k2)x2-4kx-6=0.由此入手能够求出直线l的斜率的取值范围.
(2+
|
(2-
|
| 2 |
(Ⅱ)依题意,可设直线l的方程为y=kx+2,代入双曲线C的方程并整理,得(1-k2)x2-4kx-6=0.由此入手能够求出直线l的斜率的取值范围.
解答:解:(Ⅰ)解:以O为原点,AB、OD所在直线分别为x轴、y轴,建立平面直角坐标系,
则A(-2,0),B(2,0),D(0,2),P(
,1),依题意得
|MA|-|MB|=|PA|-|PB|
=
-
=2
<|AB|=4.
∴曲线C是以原点为中心,A、B为焦点的双曲线.
设实半轴长为a,虚半轴长为b,半焦距为c,
则c=2,2a=2
,∴a2=2,b2=c2-a2=2.
∴曲线C的方程为
-
=1.
(Ⅱ)解:依题意,可设直线l的方程为y=kx+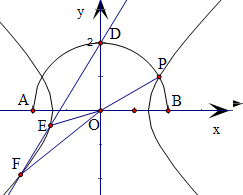 2,代入双曲线C的方程并整理,
2,代入双曲线C的方程并整理,
得(1-k2)x2-4kx-6=0.
∵直线l与双曲线C相交于不同的两点E、F,
∴
?
.
∴k∈(-
,
)且k≠±1.②
设E(x1,y1),F(x2,y2),则由①式得
|x1-x2|=
=
=
.③
当E、F在同一支上时
S△OEF=|S△ODF-S△ODE|=
|OD|•||x1|-|x2||=
|OD|•|x1-x2|;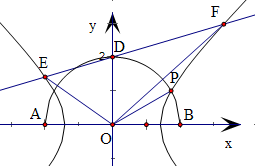
当E、F在不同支上时
S△OEF=S△ODF+S△ODE=
|OD|•(|x1|+|x2|)=
|OD|•|x1-x2|.
综上得S△OEF=
|OD|•|x1-x2|,于是由|OD|=2及③式,
得S△OEF=
.
若△OEF面积不小于2
,即S△OEF≥2
,
则有
?k2≤2,解得-
≤k≤
.④
综合②、④知,直线l的斜率的取值范围为k∈[-
,
]且k≠±1
则A(-2,0),B(2,0),D(0,2),P(
| 3 |
|MA|-|MB|=|PA|-|PB|
=
(2+
|
(2-
|
=2
| 2 |
∴曲线C是以原点为中心,A、B为焦点的双曲线.
设实半轴长为a,虚半轴长为b,半焦距为c,
则c=2,2a=2
| 2 |
∴曲线C的方程为
| x2 |
| 2 |
| y2 |
| 2 |
(Ⅱ)解:依题意,可设直线l的方程为y=kx+
 2,代入双曲线C的方程并整理,
2,代入双曲线C的方程并整理,得(1-k2)x2-4kx-6=0.
∵直线l与双曲线C相交于不同的两点E、F,
∴
|
|
∴k∈(-
| 3 |
| 3 |
设E(x1,y1),F(x2,y2),则由①式得
|x1-x2|=
| (x1+x2)2-4x1x2 |
| ||
| |1-k2| |
2
| ||||
| |1-k2| |
当E、F在同一支上时
S△OEF=|S△ODF-S△ODE|=
| 1 |
| 2 |
| 1 |
| 2 |

当E、F在不同支上时
S△OEF=S△ODF+S△ODE=
| 1 |
| 2 |
| 1 |
| 2 |
综上得S△OEF=
| 1 |
| 2 |
得S△OEF=
2
| ||||
| |1-k2| |
若△OEF面积不小于2
| 2 |
| 2 |
则有
2
| ||||
| |1-k2| |
| 2 |
| 2 |
综合②、④知,直线l的斜率的取值范围为k∈[-
| 2 |
| 2 |
点评:本小题主要考查直线、圆和双曲线等平面解析几何的基础知识,考查轨迹方程的求法、不等式的解法以及综合解题能力

练习册系列答案
相关题目
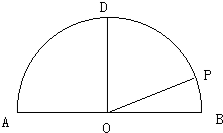
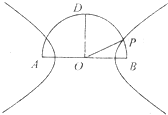 如图,在以点O为圆心,AB为直径的半圆中,D为半圆弧的中心,P为半圆弧上一点,且AB=4,∠POB=30°,双曲线C以A,B为焦点且经过点P.
如图,在以点O为圆心,AB为直径的半圆中,D为半圆弧的中心,P为半圆弧上一点,且AB=4,∠POB=30°,双曲线C以A,B为焦点且经过点P.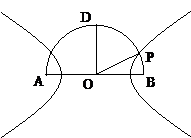
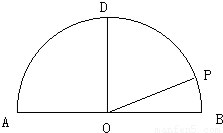 如图,在以点O为圆心,|AB|=4为直径的半圆ADB中,OD⊥AB,P是半圆弧上一点,∠POB=30°,曲线C是满足||MA|-|MB||为定值的动点M的轨迹,且曲线C过点P.
如图,在以点O为圆心,|AB|=4为直径的半圆ADB中,OD⊥AB,P是半圆弧上一点,∠POB=30°,曲线C是满足||MA|-|MB||为定值的动点M的轨迹,且曲线C过点P.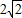 ,求直线l斜率的取值范围.
,求直线l斜率的取值范围.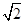 ,求直线l斜率的取值范围。
,求直线l斜率的取值范围。