题目内容
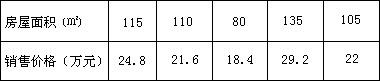
以下是某地搜集到的新房屋的销售价格y和房屋的面积x的数据：房屋面积(m2) | 115 | 110 | 80 | 135 | 105 |
销售价格(万元) | 24.8 | 21.6 | 18.4 | 29.2 | 22 |
(1)画出数据对应的散点图；
(2)求线性回归方程,并在散点图中加上回归直线；
(3)据(2)的结果估计当房屋面积为150 m2时的销售价格.
解析：(1)数据对应的散点图如图2-3-5所示：
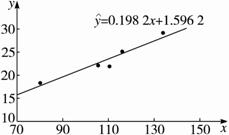
图2-3-5
(2)
=
xi=109,
(xi-
)2=1 570,
=23.2,
(xi-
)(yi-
)=311.2.
设所求回归直线方程为
=bx+a,则
b=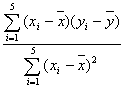
=
≈0.198 2,
a=
-b
=23.2-109×0.198 2≈1.596 2.
故所求回归直线方程为
=-0.198 2x+1.596 2.
(3)据(2),当x=150 m2时,销售价格的估计值为：
=0.198 2×150+1.596 2=31.326 2(万元).
练习册系列答案
相关题目
以下是某地搜集到的新房屋的销售价格y和房屋的面积x的数据：
（1）画出数据对应的散点图；
（2）求线性回归方程，并在散点图中加上回归直线；
（3）据（2）的结果估计当房屋面积为150m2时的销售价格．
（参考公式：
=
，
=
-
，
x2i=60975，
xiyi=115×24.8+110×21.6+80×18.4+135×29.2+105×22=12952）
| 房屋面积（m2） | 115 | 110 | 80 | 135 | 105 |
| 销售价格（万元） | 24.8 | 21.6 | 18.4 | 29.2 | 22 |
（2）求线性回归方程，并在散点图中加上回归直线；
（3）据（2）的结果估计当房屋面积为150m2时的销售价格．
（参考公式：
| ? |
| b |
| |||||||
|
| ? |
| a |
. |
| y |
| ? |
| b |
. |
| x |
| 5 |
 |
| i=1 |
| 5 |
|
| i=1 |